Question Number 106447 by Muhsang S L last updated on 05/Aug/20
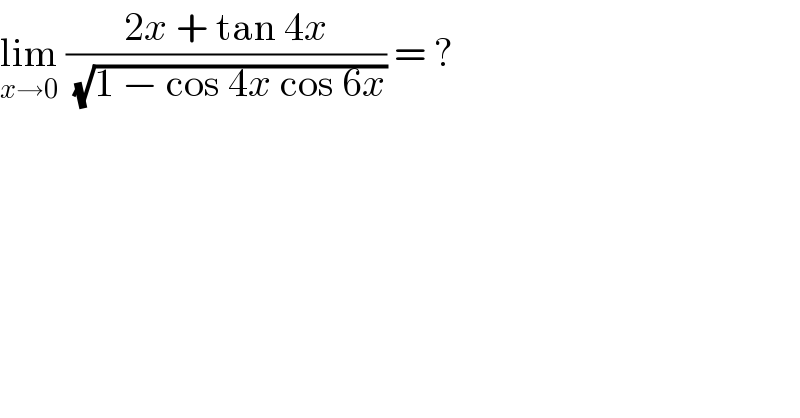
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}\:+\:\mathrm{tan}\:\mathrm{4}{x}}{\:\sqrt{\mathrm{1}\:−\:\mathrm{cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{6}{x}}}\:=\:? \\ $$
Answered by john santu last updated on 05/Aug/20
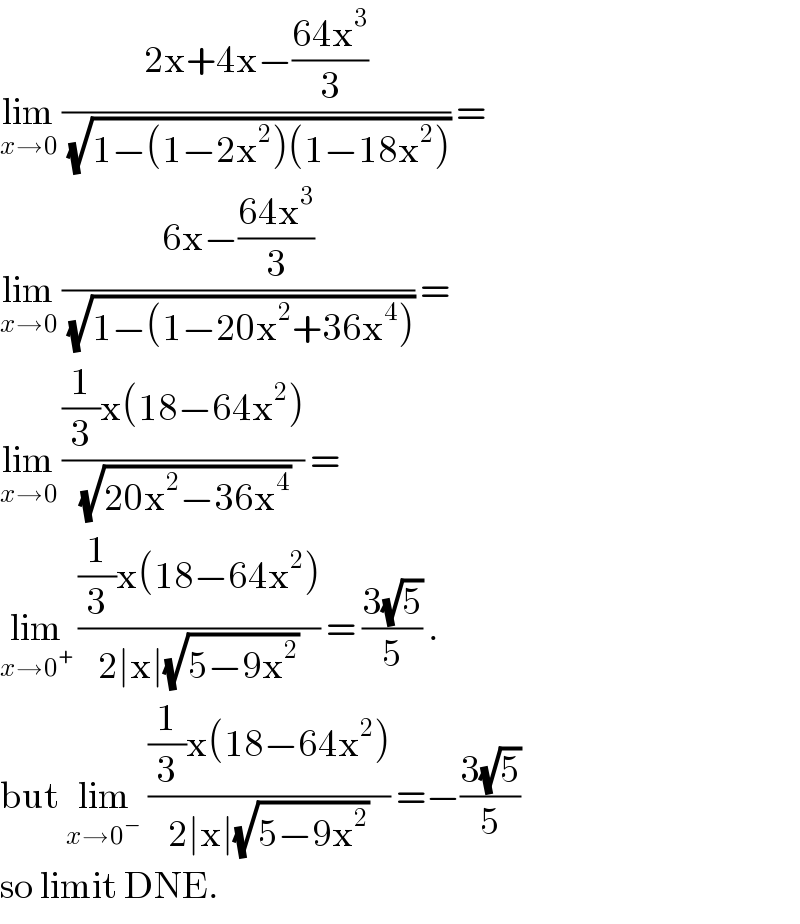
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2x}+\mathrm{4x}−\frac{\mathrm{64x}^{\mathrm{3}} }{\mathrm{3}}}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{18x}^{\mathrm{2}} \right)}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6x}−\frac{\mathrm{64x}^{\mathrm{3}} }{\mathrm{3}}}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{20x}^{\mathrm{2}} +\mathrm{36x}^{\mathrm{4}} \right)}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}\left(\mathrm{18}−\mathrm{64x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{20x}^{\mathrm{2}} −\mathrm{36x}^{\mathrm{4}} }}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}\left(\mathrm{18}−\mathrm{64x}^{\mathrm{2}} \right)}{\mathrm{2}\mid\mathrm{x}\mid\sqrt{\mathrm{5}−\mathrm{9x}^{\mathrm{2}} }}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{5}}\:. \\ $$$$\mathrm{but}\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}\left(\mathrm{18}−\mathrm{64x}^{\mathrm{2}} \right)}{\mathrm{2}\mid\mathrm{x}\mid\sqrt{\mathrm{5}−\mathrm{9x}^{\mathrm{2}} }}\:=−\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$$\mathrm{so}\:\mathrm{limit}\:\mathrm{DNE}. \\ $$
Commented by john santu last updated on 05/Aug/20

