Question Number 112311 by bemath last updated on 07/Sep/20

$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{3sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:\mathrm{2x}−\mathrm{1}}{\mathrm{x}.\mathrm{tan}\:\mathrm{2x}}}\:? \\ $$
Commented by Dwaipayan Shikari last updated on 07/Sep/20
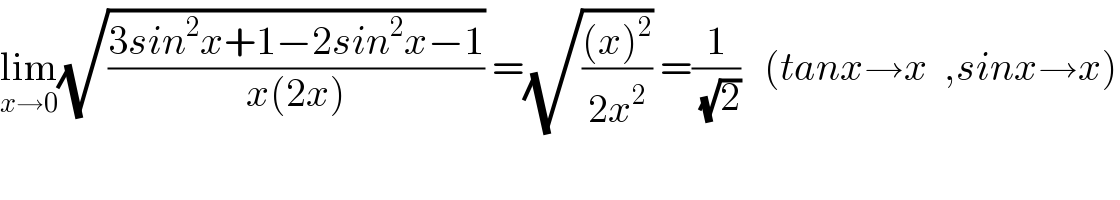
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt{\frac{\mathrm{3}{sin}^{\mathrm{2}} {x}+\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}−\mathrm{1}}{{x}\left(\mathrm{2}{x}\right)}}\:=\sqrt{\frac{\left({x}\right)^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\:\left({tanx}\rightarrow{x}\:\:,{sinx}\rightarrow{x}\right) \\ $$
Commented by malwan last updated on 07/Sep/20

$${What}\:{if}\:\:\underset{{x}\rightarrow\mathrm{0}^{−} } {{lim}}\:? \\ $$
Answered by mathmax by abdo last updated on 07/Sep/20

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\frac{\mathrm{3sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{1}}{\mathrm{xtan}\left(\mathrm{2x}\right)}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\sim\sqrt{\frac{\mathrm{3x}^{\mathrm{2}} +\mathrm{1}−\frac{\mathrm{4x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2x}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$
