Question Number 122106 by bemath last updated on 14/Nov/20
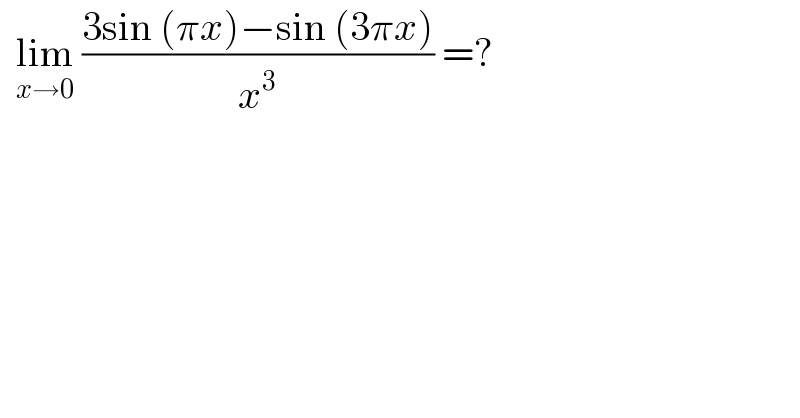
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3sin}\:\left(\pi{x}\right)−\mathrm{sin}\:\left(\mathrm{3}\pi{x}\right)}{{x}^{\mathrm{3}} }\:=? \\ $$
Answered by liberty last updated on 14/Nov/20
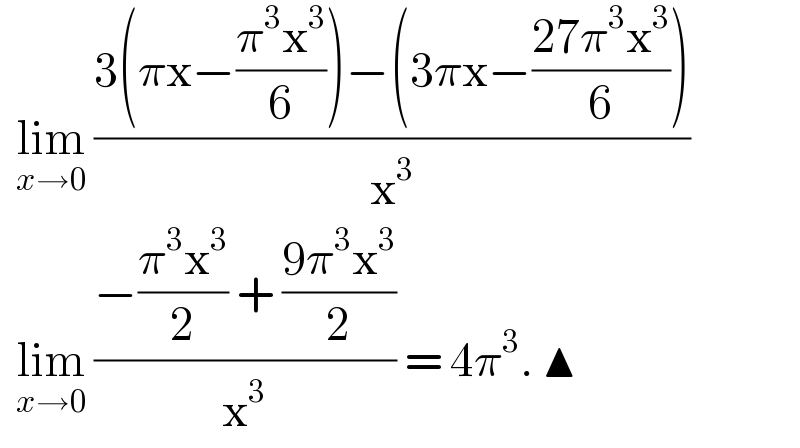
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}\left(\pi\mathrm{x}−\frac{\pi^{\mathrm{3}} \mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\mathrm{3}\pi\mathrm{x}−\frac{\mathrm{27}\pi^{\mathrm{3}} \mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\pi^{\mathrm{3}} \mathrm{x}^{\mathrm{3}} }{\mathrm{2}}\:+\:\frac{\mathrm{9}\pi^{\mathrm{3}} \mathrm{x}^{\mathrm{3}} }{\mathrm{2}}}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{4}\pi^{\mathrm{3}} .\:\blacktriangle \\ $$
Answered by Bird last updated on 14/Nov/20
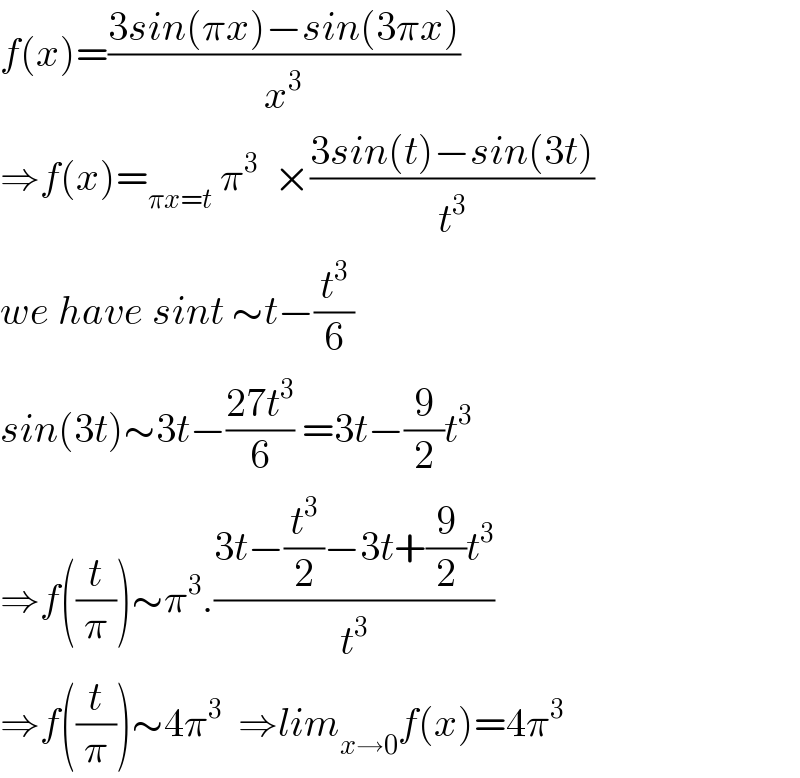
$${f}\left({x}\right)=\frac{\mathrm{3}{sin}\left(\pi{x}\right)−{sin}\left(\mathrm{3}\pi{x}\right)}{{x}^{\mathrm{3}} } \\ $$$$\Rightarrow{f}\left({x}\right)=_{\pi{x}={t}} \:\pi^{\mathrm{3}} \:\:×\frac{\mathrm{3}{sin}\left({t}\right)−{sin}\left(\mathrm{3}{t}\right)}{{t}^{\mathrm{3}} } \\ $$$${we}\:{have}\:{sint}\:\sim{t}−\frac{{t}^{\mathrm{3}} }{\mathrm{6}} \\ $$$${sin}\left(\mathrm{3}{t}\right)\sim\mathrm{3}{t}−\frac{\mathrm{27}{t}^{\mathrm{3}} }{\mathrm{6}}\:=\mathrm{3}{t}−\frac{\mathrm{9}}{\mathrm{2}}{t}^{\mathrm{3}} \\ $$$$\Rightarrow{f}\left(\frac{{t}}{\pi}\right)\sim\pi^{\mathrm{3}} .\frac{\mathrm{3}{t}−\frac{{t}^{\mathrm{3}} }{\mathrm{2}}−\mathrm{3}{t}+\frac{\mathrm{9}}{\mathrm{2}}{t}^{\mathrm{3}} }{{t}^{\mathrm{3}} } \\ $$$$\Rightarrow{f}\left(\frac{{t}}{\pi}\right)\sim\mathrm{4}\pi^{\mathrm{3}} \:\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\mathrm{4}\pi^{\mathrm{3}} \\ $$
