Question Number 128674 by bemath last updated on 09/Jan/21
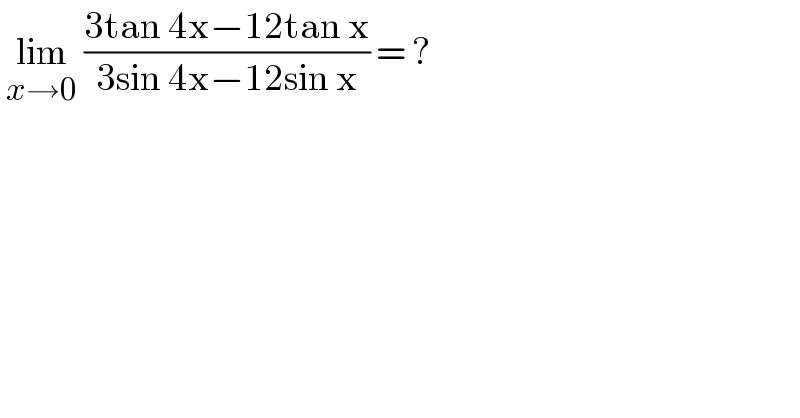
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3tan}\:\mathrm{4x}−\mathrm{12tan}\:\mathrm{x}}{\mathrm{3sin}\:\mathrm{4x}−\mathrm{12sin}\:\mathrm{x}}\:=\:? \\ $$$$ \\ $$
Answered by liberty last updated on 09/Jan/21
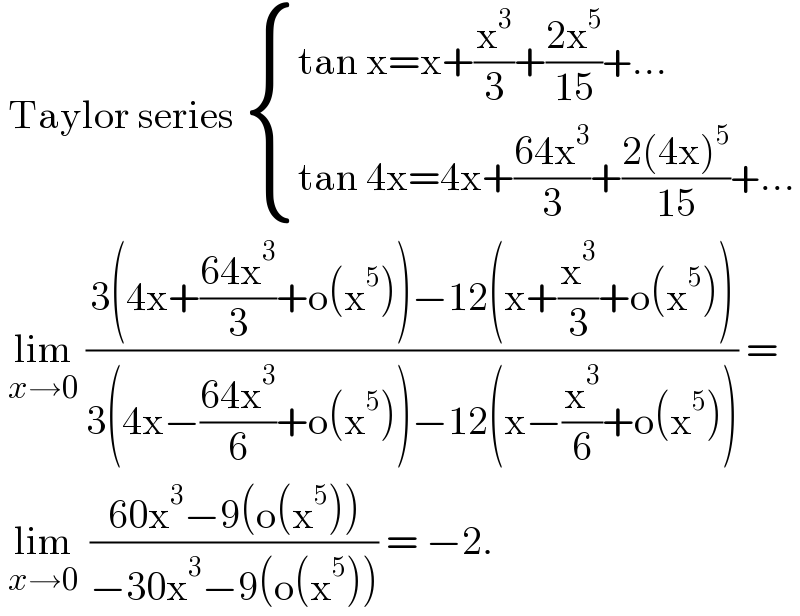
$$\:\mathrm{Taylor}\:\mathrm{series}\:\begin{cases}{\mathrm{tan}\:\mathrm{x}=\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2x}^{\mathrm{5}} }{\mathrm{15}}+…}\\{\mathrm{tan}\:\mathrm{4x}=\mathrm{4x}+\frac{\mathrm{64x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}\left(\mathrm{4x}\right)^{\mathrm{5}} }{\mathrm{15}}+…}\end{cases} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}\left(\mathrm{4x}+\frac{\mathrm{64x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)−\mathrm{12}\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)}{\mathrm{3}\left(\mathrm{4x}−\frac{\mathrm{64x}^{\mathrm{3}} }{\mathrm{6}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)−\mathrm{12}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{60x}^{\mathrm{3}} −\mathrm{9}\left(\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)}{−\mathrm{30x}^{\mathrm{3}} −\mathrm{9}\left(\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)}\:=\:−\mathrm{2}. \\ $$
