Question Number 117422 by bemath last updated on 11/Oct/20
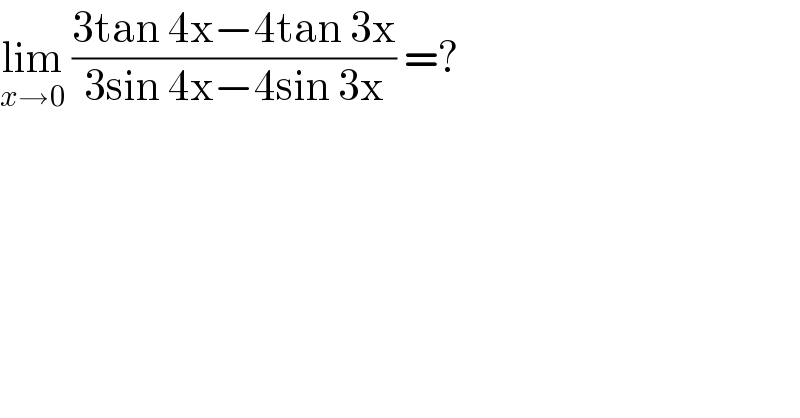
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3tan}\:\mathrm{4x}−\mathrm{4tan}\:\mathrm{3x}}{\mathrm{3sin}\:\mathrm{4x}−\mathrm{4sin}\:\mathrm{3x}}\:=? \\ $$
Answered by bobhans last updated on 11/Oct/20
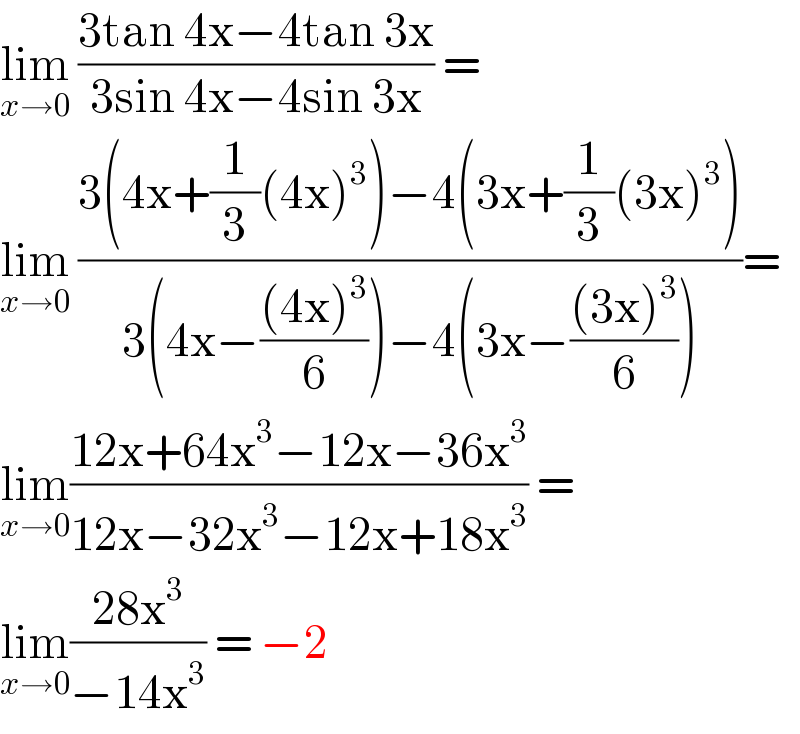
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3tan}\:\mathrm{4x}−\mathrm{4tan}\:\mathrm{3x}}{\mathrm{3sin}\:\mathrm{4x}−\mathrm{4sin}\:\mathrm{3x}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}\left(\mathrm{4x}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{4x}\right)^{\mathrm{3}} \right)−\mathrm{4}\left(\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3x}\right)^{\mathrm{3}} \right)}{\mathrm{3}\left(\mathrm{4x}−\frac{\left(\mathrm{4x}\right)^{\mathrm{3}} }{\mathrm{6}}\right)−\mathrm{4}\left(\mathrm{3x}−\frac{\left(\mathrm{3x}\right)^{\mathrm{3}} }{\mathrm{6}}\right)}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{12x}+\mathrm{64x}^{\mathrm{3}} −\mathrm{12x}−\mathrm{36x}^{\mathrm{3}} }{\mathrm{12x}−\mathrm{32x}^{\mathrm{3}} −\mathrm{12x}+\mathrm{18x}^{\mathrm{3}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{28x}^{\mathrm{3}} }{−\mathrm{14x}^{\mathrm{3}} }\:=\:−\mathrm{2} \\ $$
