Question Number 180438 by Mastermind last updated on 12/Nov/22
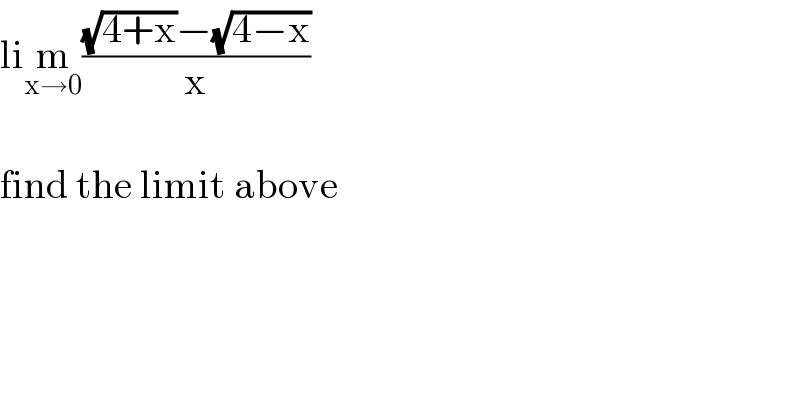
$$\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\sqrt{\mathrm{4}+\mathrm{x}}−\sqrt{\mathrm{4}−\mathrm{x}}}{\mathrm{x}} \\ $$$$ \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{above} \\ $$
Answered by Frix last updated on 12/Nov/22
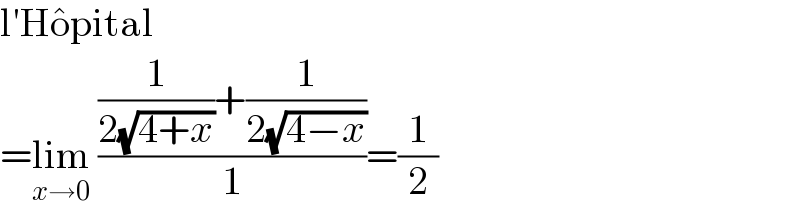
$$\mathrm{l}'\mathrm{H}\hat {\mathrm{o}pital} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{4}+{x}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{4}−{x}}}}{\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Mastermind last updated on 12/Nov/22

$$\mathrm{I}\:\mathrm{also}\:\mathrm{got}\:\mathrm{1}/\mathrm{2} \\ $$$$\mathrm{thanks} \\ $$$$ \\ $$
Answered by mr W last updated on 12/Nov/22
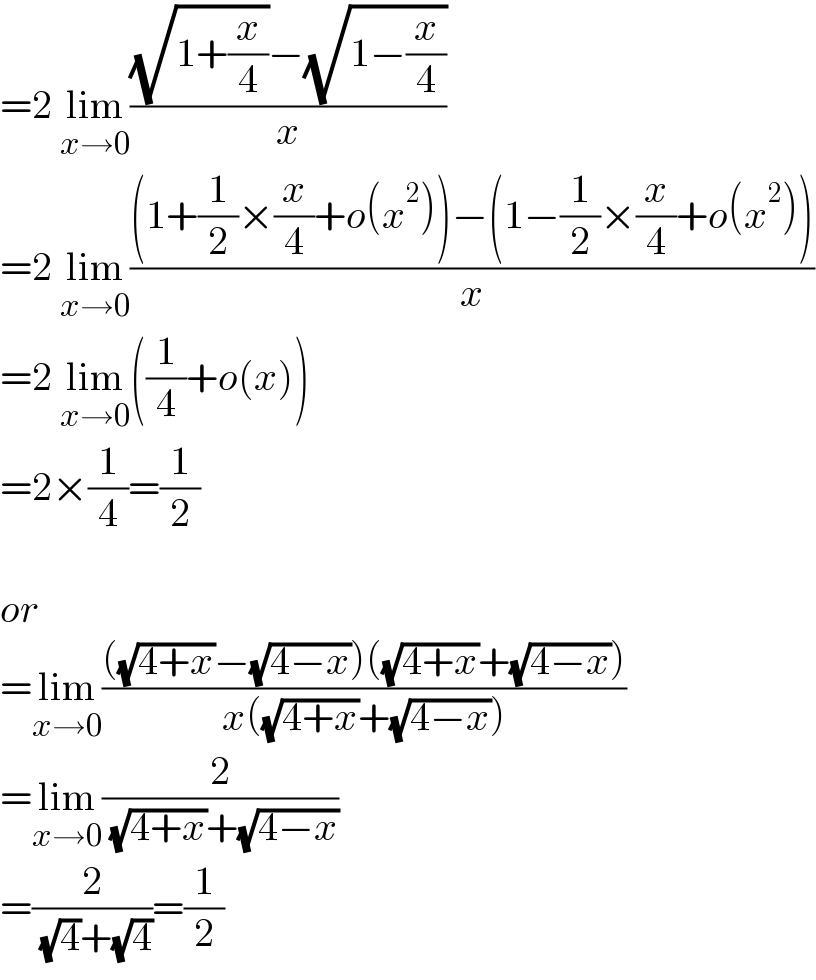
$$=\mathrm{2}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\frac{{x}}{\mathrm{4}}}−\sqrt{\mathrm{1}−\frac{{x}}{\mathrm{4}}}}{{x}} \\ $$$$=\mathrm{2}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{x}}{\mathrm{4}}+{o}\left({x}^{\mathrm{2}} \right)\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{{x}}{\mathrm{4}}+{o}\left({x}^{\mathrm{2}} \right)\right)}{{x}} \\ $$$$=\mathrm{2}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{4}}+{o}\left({x}\right)\right) \\ $$$$=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${or} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\sqrt{\mathrm{4}+{x}}−\sqrt{\mathrm{4}−{x}}\right)\left(\sqrt{\mathrm{4}+{x}}+\sqrt{\mathrm{4}−{x}}\right)}{{x}\left(\sqrt{\mathrm{4}+{x}}+\sqrt{\mathrm{4}−{x}}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{x}}+\sqrt{\mathrm{4}−{x}}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}}+\sqrt{\mathrm{4}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Mastermind last updated on 12/Nov/22
$$\mathrm{Wow}!\:\mathrm{thank}\:\mathrm{you}\:\mathrm{man} \\ $$$$ \\ $$
Answered by cortano1 last updated on 12/Nov/22
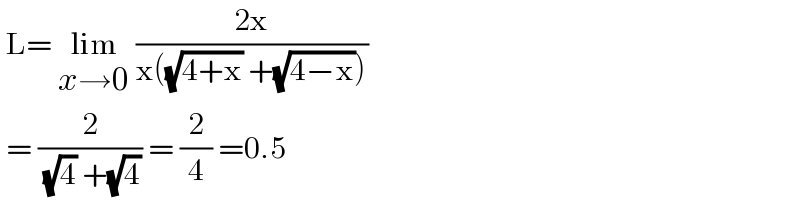
$$\:\mathrm{L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2x}}{\mathrm{x}\left(\sqrt{\mathrm{4}+\mathrm{x}}\:+\sqrt{\mathrm{4}−\mathrm{x}}\right)} \\ $$$$\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}}\:+\sqrt{\mathrm{4}}}\:=\:\frac{\mathrm{2}}{\mathrm{4}}\:=\mathrm{0}.\mathrm{5} \\ $$
Commented by Mastermind last updated on 12/Nov/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{boss} \\ $$
