Question Number 148323 by liberty last updated on 27/Jul/21
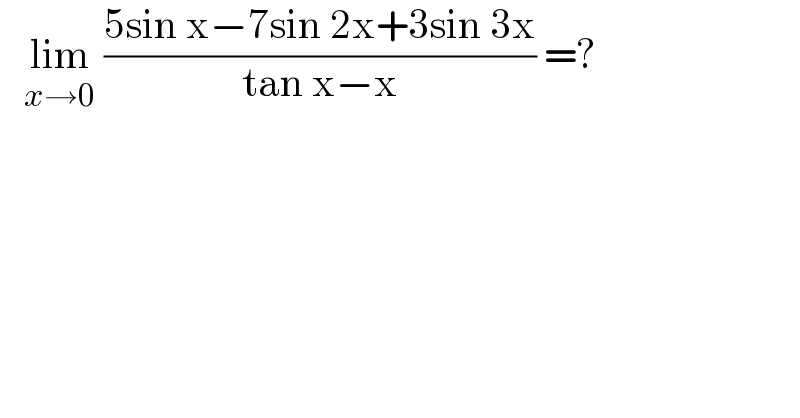
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5sin}\:\mathrm{x}−\mathrm{7sin}\:\mathrm{2x}+\mathrm{3sin}\:\mathrm{3x}}{\mathrm{tan}\:\mathrm{x}−\mathrm{x}}\:=? \\ $$
Answered by EDWIN88 last updated on 27/Jul/21

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5cos}\:{x}−\mathrm{14cos}\:\mathrm{2}{x}+\mathrm{9cos}\:\mathrm{3}{x}}{\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5cos}\:{x}−\mathrm{14}\left(\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}\right)+\mathrm{9}\left(\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}\right)}{\left(\mathrm{sec}\:{x}−\mathrm{1}\right)\left(\mathrm{sec}\:{x}+\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5cos}\:{x}−\mathrm{28cos}\:^{\mathrm{2}} {x}+\mathrm{14}+\mathrm{36cos}\:^{\mathrm{3}} {x}−\mathrm{27cos}\:{x}}{\left(\mathrm{sec}\:{x}−\mathrm{1}\right)\left(\mathrm{sec}\:{x}+\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{36cos}\:^{\mathrm{3}} {x}−\mathrm{28cos}\:^{\mathrm{2}} {x}−\mathrm{22cos}\:{x}+\mathrm{14}}{\left(\mathrm{sec}\:{x}−\mathrm{1}\right)\left(\mathrm{sec}\:{x}+\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{cos}\:{x}−\mathrm{1}\right)\left(\mathrm{36cos}\:^{\mathrm{2}} {x}+\mathrm{8cos}\:{x}−\mathrm{14}\right)}{\left(\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{cos}\:{x}}\right)\left(\mathrm{sec}\:{x}+\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}\left(\mathrm{36cos}\:^{\mathrm{2}} {x}+\mathrm{8cos}\:{x}−\mathrm{14}\right)}{\mathrm{sec}\:{x}+\mathrm{1}}\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{x}−\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:{x}} \\ $$$$=\:−\frac{\mathrm{36}+\mathrm{8}−\mathrm{14}}{\mathrm{2}}=−\mathrm{15}\:. \\ $$
Answered by lyubita last updated on 27/Jul/21
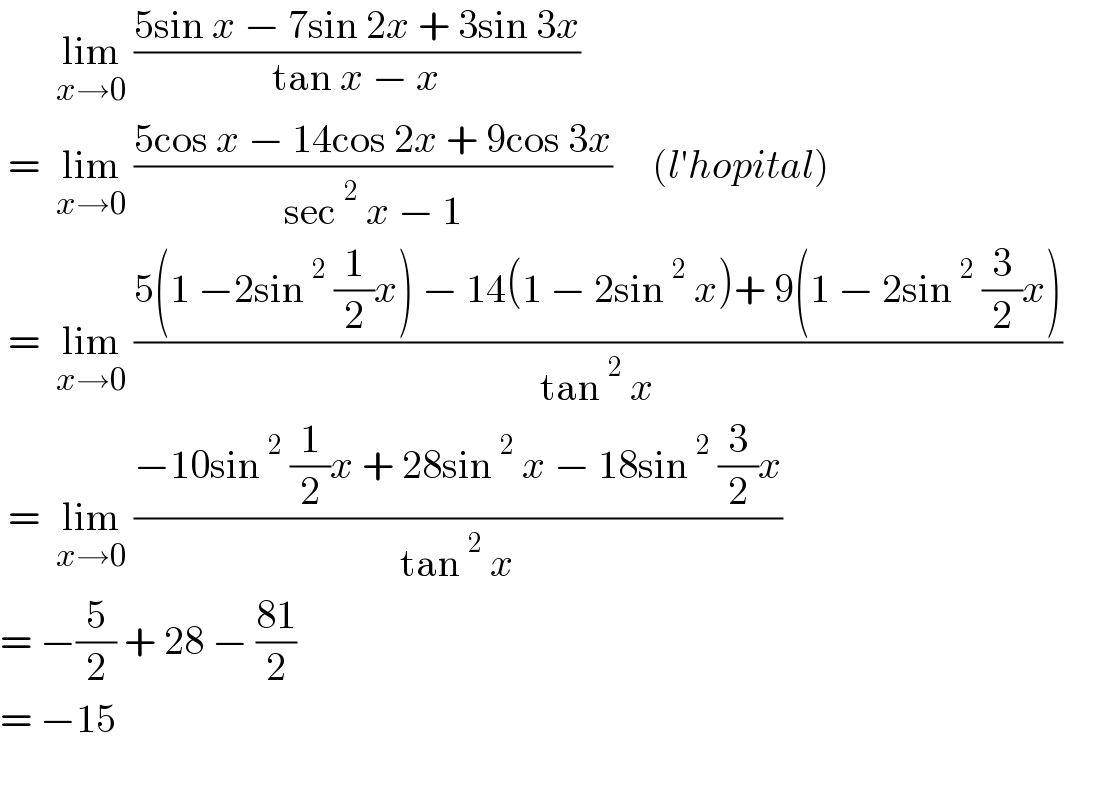
$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5sin}\:{x}\:−\:\mathrm{7sin}\:\mathrm{2}{x}\:+\:\mathrm{3sin}\:\mathrm{3}{x}}{\mathrm{tan}\:{x}\:−\:{x}} \\ $$$$\:=\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5cos}\:{x}\:−\:\mathrm{14cos}\:\mathrm{2}{x}\:+\:\mathrm{9cos}\:\mathrm{3}{x}}{\mathrm{sec}\:^{\mathrm{2}} \:{x}\:−\:\mathrm{1}}\:\:\:\:\:\left({l}'{hopital}\right)\:\:\:\: \\ $$$$\:=\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}\left(\mathrm{1}\:−\mathrm{2sin}\:^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}}{x}\right)\:−\:\mathrm{14}\left(\mathrm{1}\:−\:\mathrm{2sin}\:^{\mathrm{2}} \:{x}\right)+\:\mathrm{9}\left(\mathrm{1}\:−\:\mathrm{2sin}\:^{\mathrm{2}} \:\frac{\mathrm{3}}{\mathrm{2}}{x}\right)}{\mathrm{tan}\:^{\mathrm{2}} \:{x}}\:\:\:\: \\ $$$$\:=\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{10sin}\:^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\:\mathrm{28sin}\:^{\mathrm{2}} \:{x}\:−\:\mathrm{18sin}\:^{\mathrm{2}} \:\frac{\mathrm{3}}{\mathrm{2}}{x}}{\mathrm{tan}\:^{\mathrm{2}} \:{x}}\:\:\:\: \\ $$$$=\:−\frac{\mathrm{5}}{\mathrm{2}}\:+\:\mathrm{28}\:−\:\frac{\mathrm{81}}{\mathrm{2}} \\ $$$$=\:−\mathrm{15} \\ $$$$ \\ $$
