Menu Close

lim-x-0-5sin-x-sin-3x-cos-2x-cos-3x-sin-2x-x-3-

Tinku Tara 0 Comments
Pin




Question Number 162364 by cortano last updated on 29/Dec/21
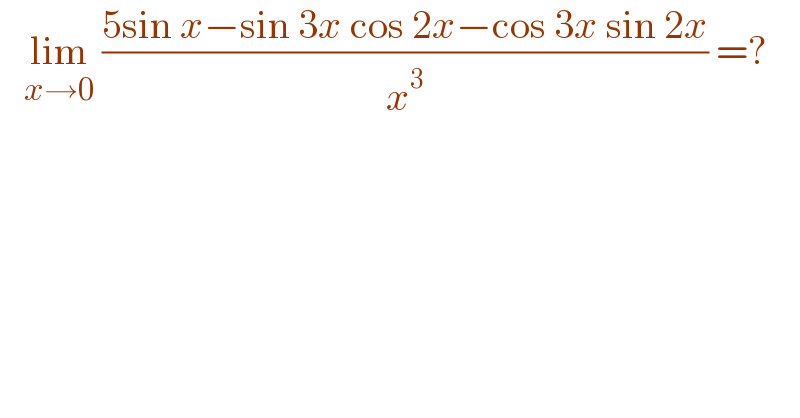
lim_(x→0) ((5sin x−sin 3x cos 2x−cos 3x sin 2x)/x^3 ) =?
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}\:\mathrm{cos}\:\mathrm{2}{x}−\mathrm{cos}\:\mathrm{3}{x}\:\mathrm{sin}\:\mathrm{2}{x}}{{x}^{\mathrm{3}} }\:=? \\ $$
Commented by blackmamba last updated on 29/Dec/21
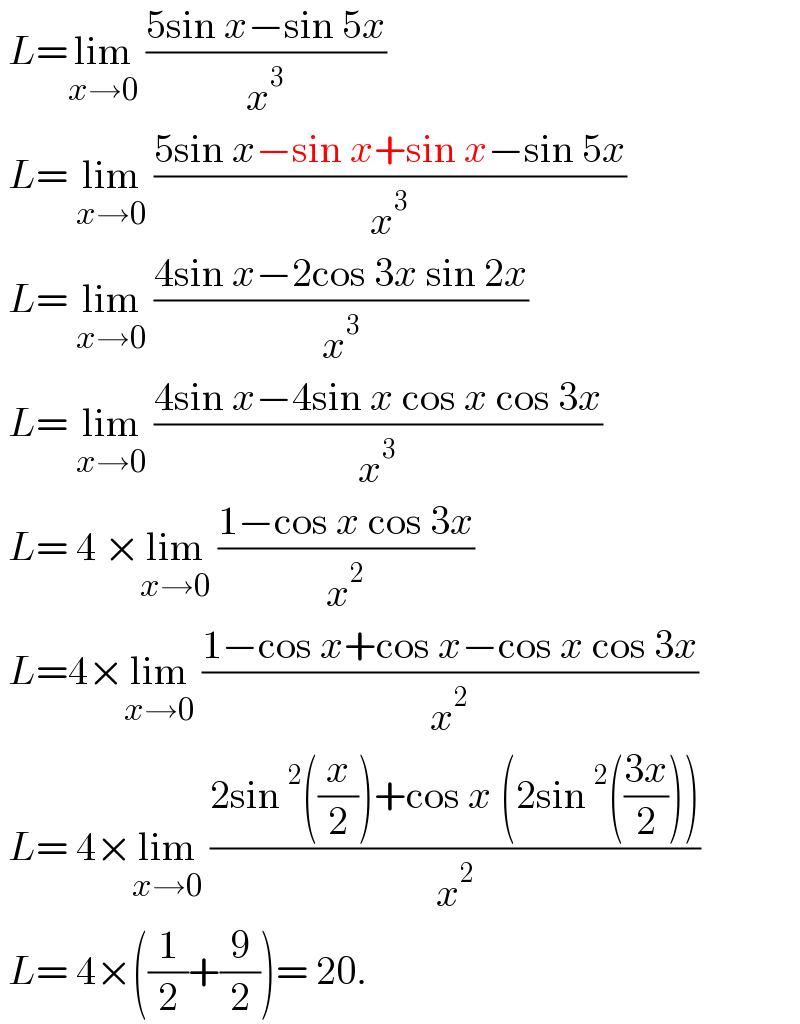
L=lim_(x→0) ((5sin x−sin 5x)/x^3 ) L= lim_(x→0) ((5sin x−sin x+sin x−sin 5x)/x^3 ) L= lim_(x→0) ((4sin x−2cos 3x sin 2x)/x^3 ) L= lim_(x→0) ((4sin x−4sin x cos x cos 3x)/x^3 ) L= 4 ×lim_(x→0) ((1−cos x cos 3x)/x^2 ) L=4×lim_(x→0) ((1−cos x+cos x−cos x cos 3x)/x^2 ) L= 4×lim_(x→0) ((2sin^2 ((x/2))+cos x (2sin^2 (((3x)/2))))/x^2 ) L= 4×((1/2)+(9/2))= 20.
$$\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5sin}\:{x}−\mathrm{sin}\:\mathrm{5}{x}}{{x}^{\mathrm{3}} } \\ $$$$\:{L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5sin}\:{x}−\mathrm{sin}\:{x}+\mathrm{sin}\:{x}−\mathrm{sin}\:\mathrm{5}{x}}{{x}^{\mathrm{3}} }\: \\ $$$$\:{L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4sin}\:{x}−\mathrm{2cos}\:\mathrm{3}{x}\:\mathrm{sin}\:\mathrm{2}{x}}{{x}^{\mathrm{3}} } \\ $$$$\:{L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4sin}\:{x}−\mathrm{4sin}\:{x}\:\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{3}{x}}{{x}^{\mathrm{3}} } \\ $$$$\:{L}=\:\mathrm{4}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{3}{x}}{{x}^{\mathrm{2}} }\: \\ $$$$\:{L}=\mathrm{4}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}+\mathrm{cos}\:{x}−\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{3}{x}}{{x}^{\mathrm{2}} } \\ $$$$\:{L}=\:\mathrm{4}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{cos}\:{x}\:\left(\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\right)}{{x}^{\mathrm{2}} } \\ $$$$\:{L}=\:\mathrm{4}×\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}\right)=\:\mathrm{20}. \\ $$
Answered by aleks041103 last updated on 29/Dec/21
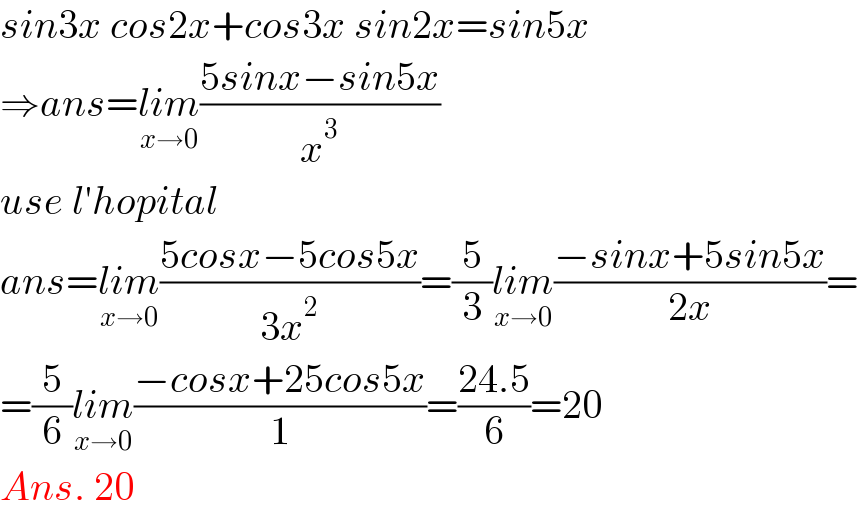
sin3x cos2x+cos3x sin2x=sin5x ⇒ans=lim_(x→0) ((5sinx−sin5x)/x^3 ) use l′hopital ans=lim_(x→0) ((5cosx−5cos5x)/(3x^2 ))=(5/3)lim_(x→0) ((−sinx+5sin5x)/(2x))= =(5/6)lim_(x→0) ((−cosx+25cos5x)/1)=((24.5)/6)=20 Ans. 20
$${sin}\mathrm{3}{x}\:{cos}\mathrm{2}{x}+{cos}\mathrm{3}{x}\:{sin}\mathrm{2}{x}={sin}\mathrm{5}{x} \\ $$$$\Rightarrow{ans}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{5}{sinx}−{sin}\mathrm{5}{x}}{{x}^{\mathrm{3}} } \\ $$$${use}\:{l}'{hopital} \\ $$$${ans}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{5}{cosx}−\mathrm{5}{cos}\mathrm{5}{x}}{\mathrm{3}{x}^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{−{sinx}+\mathrm{5}{sin}\mathrm{5}{x}}{\mathrm{2}{x}}= \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{−{cosx}+\mathrm{25}{cos}\mathrm{5}{x}}{\mathrm{1}}=\frac{\mathrm{24}.\mathrm{5}}{\mathrm{6}}=\mathrm{20} \\ $$$${Ans}.\:\mathrm{20} \\ $$
Answered by bobhans last updated on 29/Dec/21
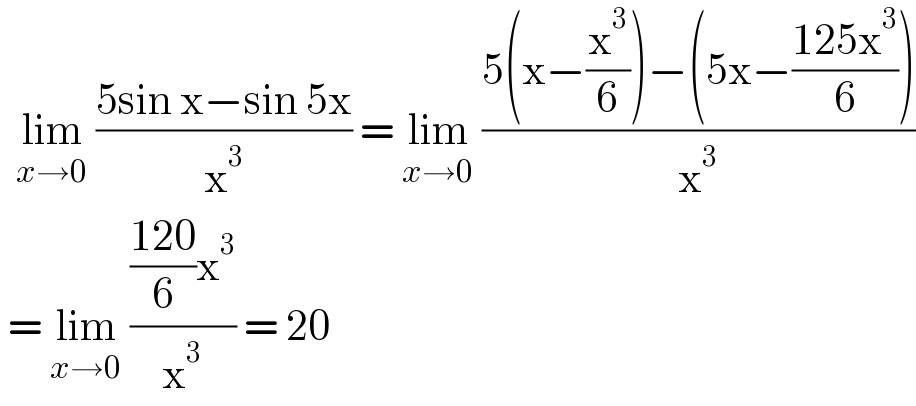
lim_(x→0) ((5sin x−sin 5x)/x^3 ) = lim_(x→0) ((5(x−(x^3 /6))−(5x−((125x^3 )/6)))/x^3 ) = lim_(x→0) ((((120)/6)x^3 )/x^3 ) = 20
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5sin}\:\mathrm{x}−\mathrm{sin}\:\mathrm{5x}}{\mathrm{x}^{\mathrm{3}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\mathrm{5x}−\frac{\mathrm{125x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{120}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{20} \\ $$
Commented by aleks041103 last updated on 29/Dec/21
I think you still need to show that the contribution of the rest of the teylor series is 0
$${I}\:{think}\:{you}\:{still}\:{need}\:{to}\:{show}\:{that}\:{the} \\ $$$${contribution}\:{of}\:{the}\:{rest}\:{of}\:{the}\:{teylor} \\ $$$${series}\:{is}\:\mathrm{0} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *