Question Number 185438 by mathlove last updated on 21/Jan/23
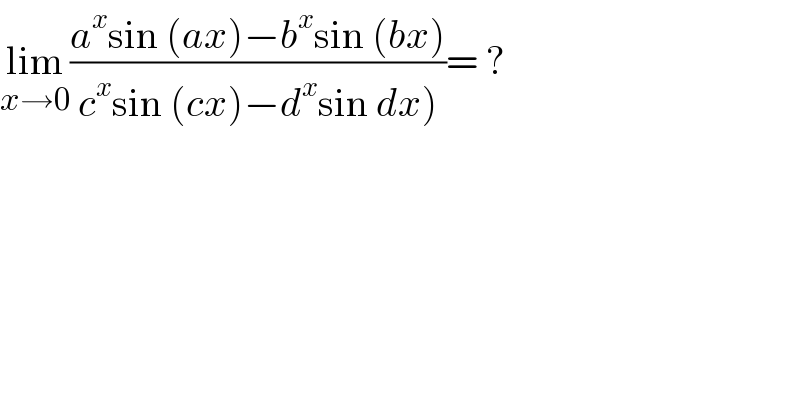
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}^{{x}} \mathrm{sin}\:\left({ax}\right)−{b}^{{x}} \mathrm{sin}\:\left({bx}\right)}{\left.{c}^{{x}} \mathrm{sin}\:\left({cx}\right)−{d}^{{x}} \mathrm{sin}\:{dx}\right)}=\:? \\ $$
Answered by hmr last updated on 21/Jan/23
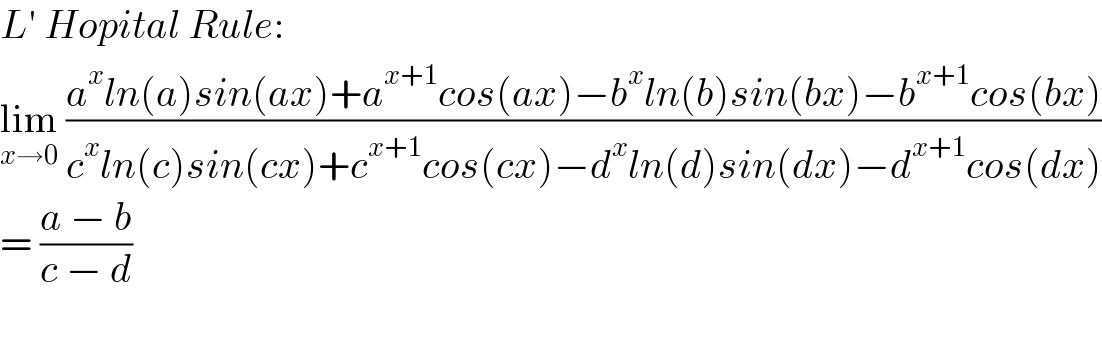
$${L}'\:{Hopital}\:{Rule}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{a}^{{x}} {ln}\left({a}\right){sin}\left({ax}\right)+{a}^{{x}+\mathrm{1}} {cos}\left({ax}\right)−{b}^{{x}} {ln}\left({b}\right){sin}\left({bx}\right)−{b}^{{x}+\mathrm{1}} {cos}\left({bx}\right)}{{c}^{{x}} {ln}\left({c}\right){sin}\left({cx}\right)+{c}^{{x}+\mathrm{1}} {cos}\left({cx}\right)−{d}^{{x}} {ln}\left({d}\right){sin}\left({dx}\right)−{d}^{{x}+\mathrm{1}} {cos}\left({dx}\right)} \\ $$$$=\:\frac{{a}\:−\:{b}}{{c}\:−\:{d}} \\ $$$$ \\ $$
