Question Number 104348 by bemath last updated on 21/Jul/20
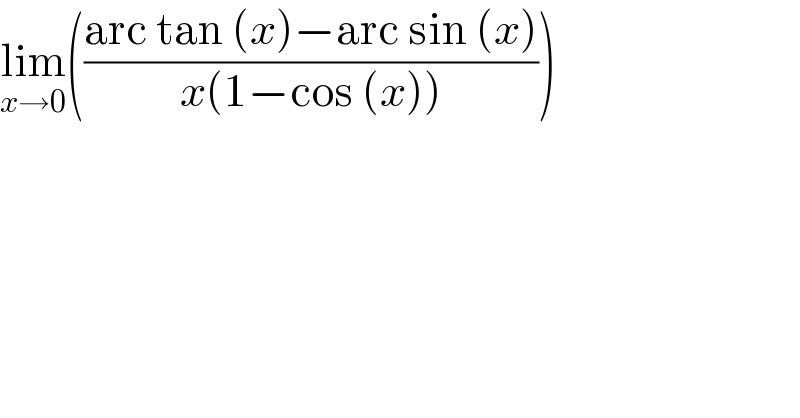
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{arc}\:\mathrm{tan}\:\left({x}\right)−\mathrm{arc}\:\mathrm{sin}\:\left({x}\right)}{{x}\left(\mathrm{1}−\mathrm{cos}\:\left({x}\right)\right)}\right) \\ $$
Answered by john santu last updated on 21/Jul/20
![L′Hopital rule lim_(x→0) [ ((tan^(−1) (x)−sin^(−1) (x))/(2x sin^2 ((x/2)))) ]= lim_(x→0) [(((1/(1+x^2 )) −(1/( (√(1−x^2 )))))/(2sin^2 ((x/2))+xsin x)) ]= lim_(x→0) [(((1+x^2 )^(−1) −(1−x^2 )^(−1/2) )/((x^2 /2)+x^2 )) ]= lim_(x→0) [(((1−x^2 )−(1+(x^2 /2)))/((3/2)x^2 ))] = lim_(x→0) [((−((3x^2 )/2))/((3/2)x^2 )) ] = −1 (JS ⊛ )](https://www.tinkutara.com/question/Q104349.png)
$${L}'{Hopital}\:{rule}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}{\mathrm{2}{x}\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\:\right]= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+{x}\mathrm{sin}\:{x}}\:\right]= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\mathrm{1}} −\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\mathrm{1}/\mathrm{2}} }{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}^{\mathrm{2}} }\:\right]= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} }\right]\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}}{\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} }\:\right]\:=\:−\mathrm{1}\:\:\left({JS}\:\circledast\:\right)\: \\ $$
Answered by OlafThorendsen last updated on 21/Jul/20
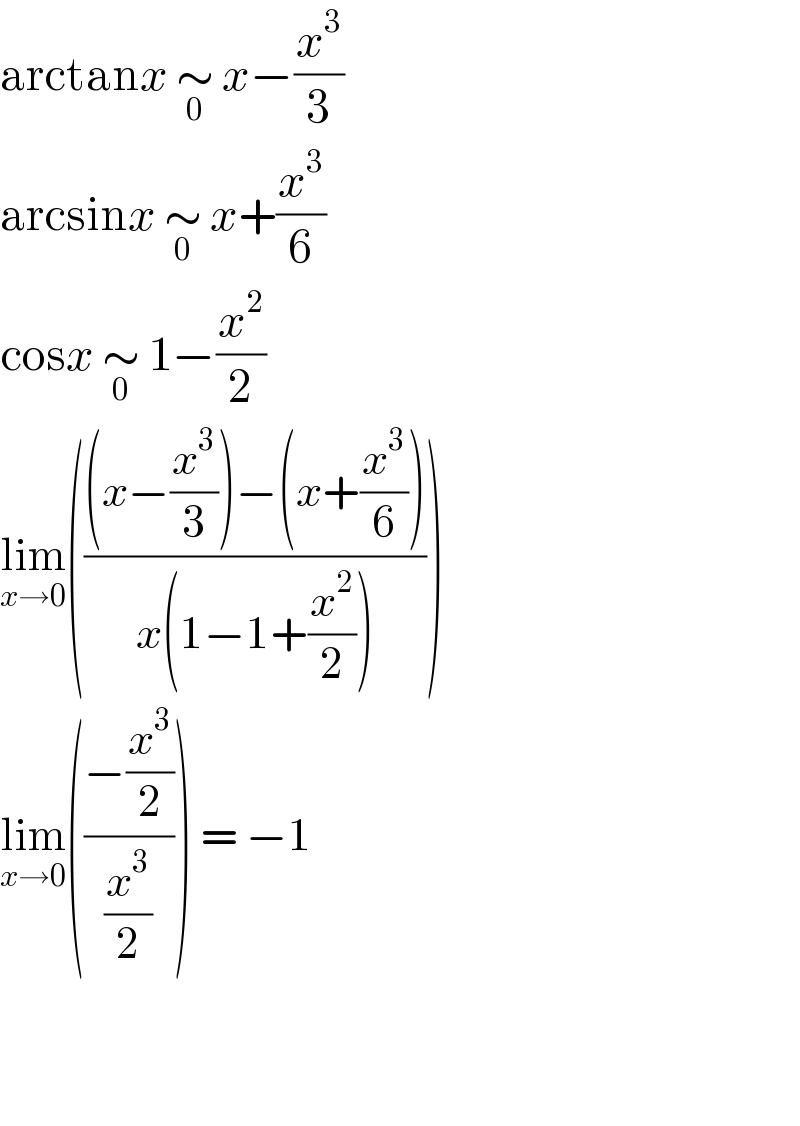
$$\mathrm{arctan}{x}\:\underset{\mathrm{0}} {\sim}\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\mathrm{arcsin}{x}\:\underset{\mathrm{0}} {\sim}\:{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\mathrm{cos}{x}\:\underset{\mathrm{0}} {\sim}\:\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)−\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{{x}\left(\mathrm{1}−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}}{\frac{{x}^{\mathrm{3}} }{\mathrm{2}}}\right)\:=\:−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jul/20
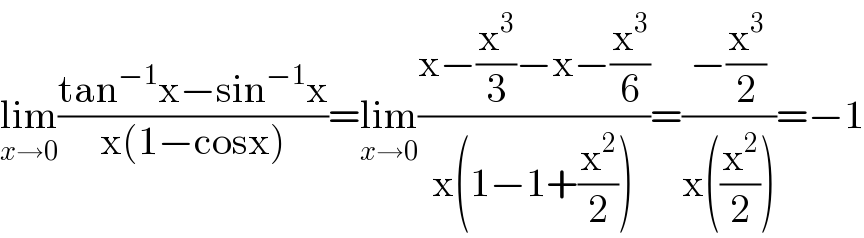
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{x}−\mathrm{sin}^{−\mathrm{1}} \mathrm{x}}{\mathrm{x}\left(\mathrm{1}−\mathrm{cosx}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{x}\left(\mathrm{1}−\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)}=\frac{−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}}{\mathrm{x}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)}=−\mathrm{1} \\ $$
