Menu Close

lim-x-0-arctan-x-arcsin-x-x-

Tinku Tara 0 Comments
Pin




Question Number 176213 by cortano1 last updated on 15/Sep/22
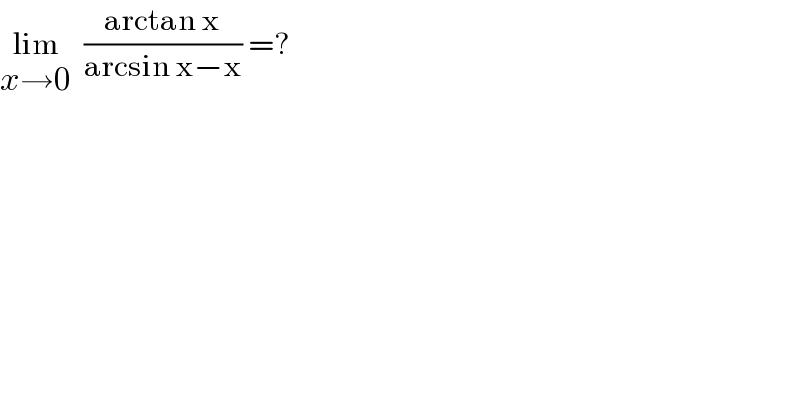
lim_(x→0) ((arctan x)/(arcsin x−x)) =?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{arctan}\:\mathrm{x}}{\mathrm{arcsin}\:\mathrm{x}−\mathrm{x}}\:=? \\ $$
Answered by flamable last updated on 15/Sep/22
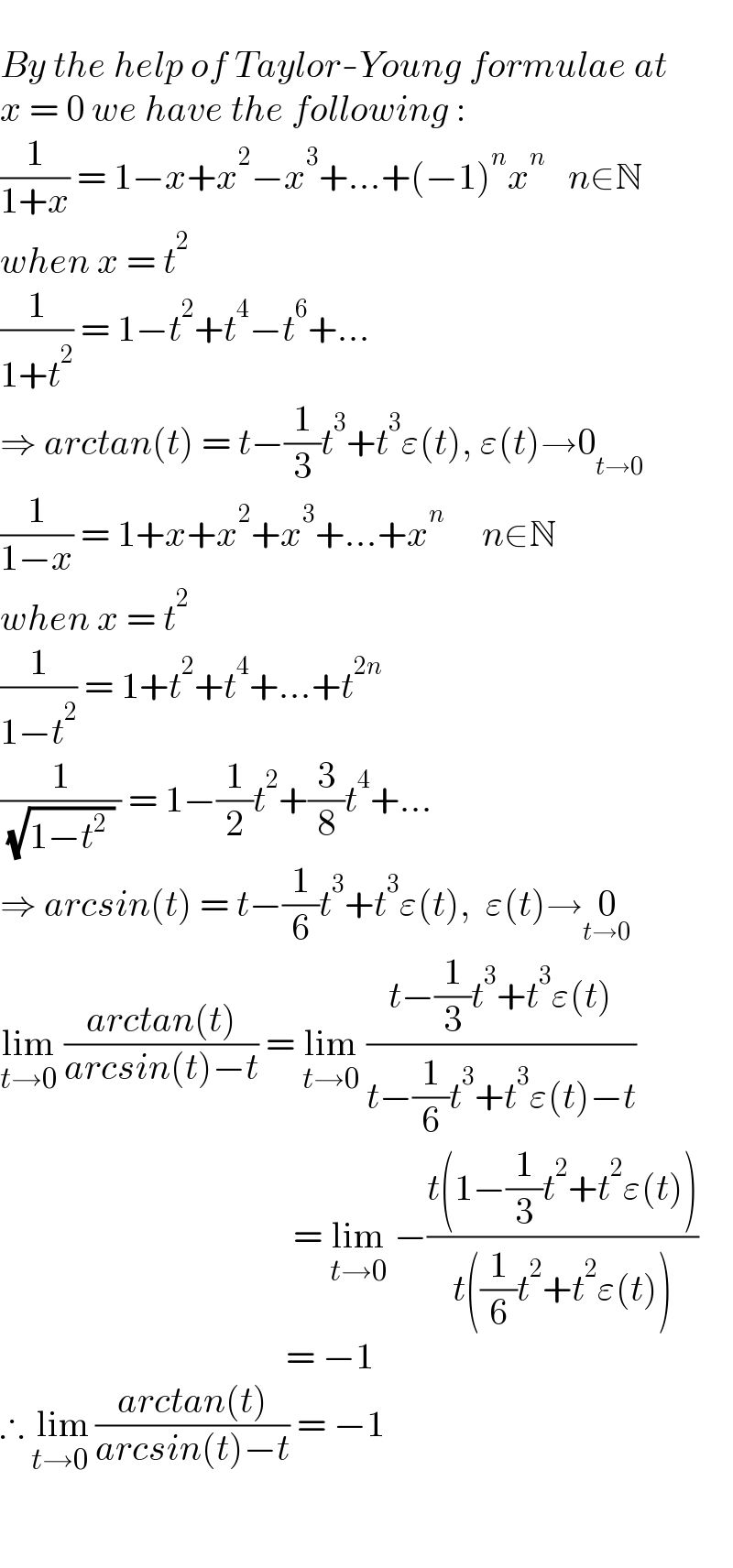
By the help of Taylor-Young formulae at x = 0 we have the following : (1/(1+x)) = 1−x+x^2 −x^3 +...+(−1)^n x^n n∈N when x = t^2 (1/(1+t^2 )) = 1−t^2 +t^4 −t^6 +... ⇒ arctan(t) = t−(1/3)t^3 +t^3 ε(t), ε(t)→0_(t→0) (1/(1−x)) = 1+x+x^2 +x^3 +...+x^n n∈N when x = t^2 (1/(1−t^2 )) = 1+t^2 +t^4 +...+t^(2n) (1/( (√(1−t^2 )) )) = 1−(1/2)t^2 +(3/8)t^4 +... ⇒ arcsin(t) = t−(1/6)t^3 +t^3 ε(t), ε(t)→0_(t→0) lim_(t→0) ((arctan(t))/(arcsin(t)−t)) = lim_(t→0) ((t−(1/3)t^3 +t^3 ε(t))/(t−(1/6)t^3 +t^3 ε(t)−t)) = lim_(t→0) −((t(1−(1/3)t^2 +t^2 ε(t)))/(t((1/6)t^2 +t^2 ε(t)))) = −1 ∴ lim_(t→0 ) ((arctan(t))/(arcsin(t)−t)) = −1
$$ \\ $$$${By}\:{the}\:{help}\:{of}\:{Taylor}-{Young}\:{formulae}\:{at}\: \\ $$$${x}\:=\:\mathrm{0}\:{we}\:{have}\:{the}\:{following}\:: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\:\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +…+\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\:\:{n}\in\mathbb{N} \\ $$$${when}\:{x}\:=\:{t}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\mathrm{1}−{t}^{\mathrm{2}} +{t}^{\mathrm{4}} −{t}^{\mathrm{6}} +… \\ $$$$\Rightarrow\:{arctan}\left({t}\right)\:=\:{t}−\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{3}} +{t}^{\mathrm{3}} \varepsilon\left({t}\right),\:\varepsilon\left({t}\right)\rightarrow\mathrm{0}_{{t}\rightarrow\mathrm{0}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{{n}} \:\:\:\:\:{n}\in\mathbb{N} \\ $$$${when}\:{x}\:=\:{t}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }\:=\:\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{4}} +…+{t}^{\mathrm{2}{n}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} \:}\:}\:=\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}{t}^{\mathrm{4}} +… \\ $$$$\Rightarrow\:{arcsin}\left({t}\right)\:=\:{t}−\frac{\mathrm{1}}{\mathrm{6}}{t}^{\mathrm{3}} +{t}^{\mathrm{3}} \varepsilon\left({t}\right),\:\:\varepsilon\left({t}\right)\rightarrow\underset{{t}\rightarrow\mathrm{0}} {\mathrm{0}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{arctan}\left({t}\right)}{{arcsin}\left({t}\right)−{t}}\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{t}−\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{3}} +{t}^{\mathrm{3}} \varepsilon\left({t}\right)}{{t}−\frac{\mathrm{1}}{\mathrm{6}}{t}^{\mathrm{3}} +{t}^{\mathrm{3}} \varepsilon\left({t}\right)−{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:−\frac{{t}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{2}} +{t}^{\mathrm{2}} \varepsilon\left({t}\right)\right)}{{t}\left(\frac{\mathrm{1}}{\mathrm{6}}{t}^{\mathrm{2}} +{t}^{\mathrm{2}} \varepsilon\left({t}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{1} \\ $$$$\therefore\:\underset{{t}\rightarrow\mathrm{0}\:} {\mathrm{lim}}\frac{{arctan}\left({t}\right)}{{arcsin}\left({t}\right)−{t}}\:=\:−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Commented by cortano1 last updated on 16/Sep/22
No
$$\mathrm{No} \\ $$
Commented by Tawa11 last updated on 25/Sep/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *