Question Number 91930 by Ozoda last updated on 03/May/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}cos}\:\frac{\mathrm{1}}{{x}}= \\ $$
Commented by mr W last updated on 03/May/20
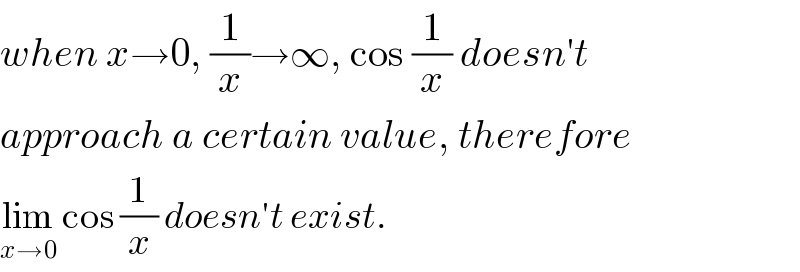
$${when}\:{x}\rightarrow\mathrm{0},\:\frac{\mathrm{1}}{{x}}\rightarrow\infty,\:\mathrm{cos}\:\frac{\mathrm{1}}{{x}}\:{doesn}'{t} \\ $$$${approach}\:{a}\:{certain}\:{value},\:{therefore} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{cos}\:\frac{\mathrm{1}}{{x}}\:{doesn}'{t}\:{exist}. \\ $$
Commented by turbo msup by abdo last updated on 03/May/20
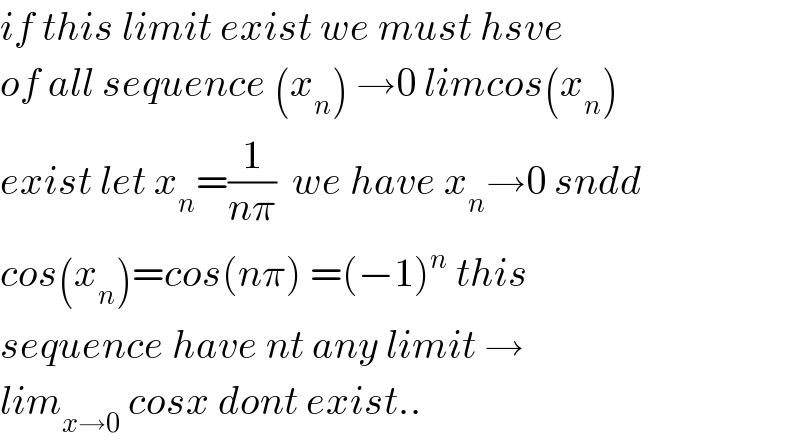
$${if}\:{this}\:{limit}\:{exist}\:{we}\:{must}\:{hsve} \\ $$$${of}\:{all}\:{sequence}\:\left({x}_{{n}} \right)\:\rightarrow\mathrm{0}\:{limcos}\left({x}_{{n}} \right) \\ $$$${exist}\:{let}\:{x}_{{n}} =\frac{\mathrm{1}}{{n}\pi}\:\:{we}\:{have}\:{x}_{{n}} \rightarrow\mathrm{0}\:{sndd} \\ $$$${cos}\left({x}_{{n}} \right)={cos}\left({n}\pi\right)\:=\left(−\mathrm{1}\right)^{{n}} \:{this} \\ $$$${sequence}\:{have}\:{nt}\:{any}\:{limit}\:\rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:{cosx}\:{dont}\:{exist}.. \\ $$
