Question Number 104838 by bramlex last updated on 24/Jul/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\:^{\mathrm{3}} \left(\mathrm{8}{x}\right)−\mathrm{1}}{\mathrm{6}{x}^{\mathrm{2}} }\:? \\ $$
Answered by john santu last updated on 24/Jul/20
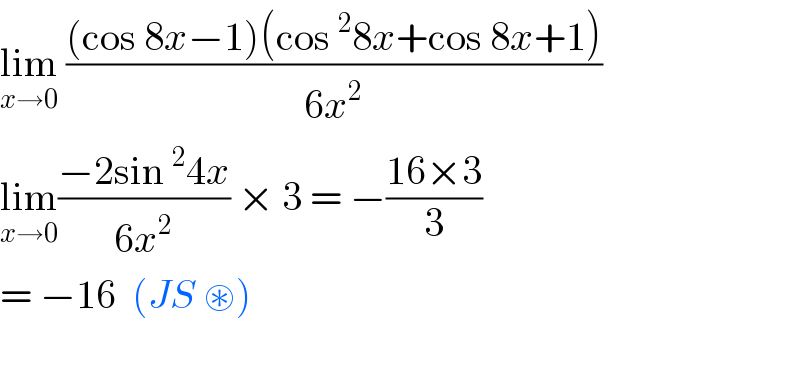
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:\mathrm{8}{x}−\mathrm{1}\right)\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{8}{x}+\mathrm{cos}\:\mathrm{8}{x}+\mathrm{1}\right)}{\mathrm{6}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{4}{x}}{\mathrm{6}{x}^{\mathrm{2}} }\:×\:\mathrm{3}\:=\:−\frac{\mathrm{16}×\mathrm{3}}{\mathrm{3}} \\ $$$$=\:−\mathrm{16}\:\:\left({JS}\:\circledast\right)\: \\ $$$$ \\ $$
Commented by bramlex last updated on 24/Jul/20

$$\spadesuit\blacklozenge \\ $$
