Menu Close

lim-x-0-cos-sin-x-cos-x-x-4-

Tinku Tara 0 Comments
Pin




Question Number 104899 by bramlex last updated on 24/Jul/20
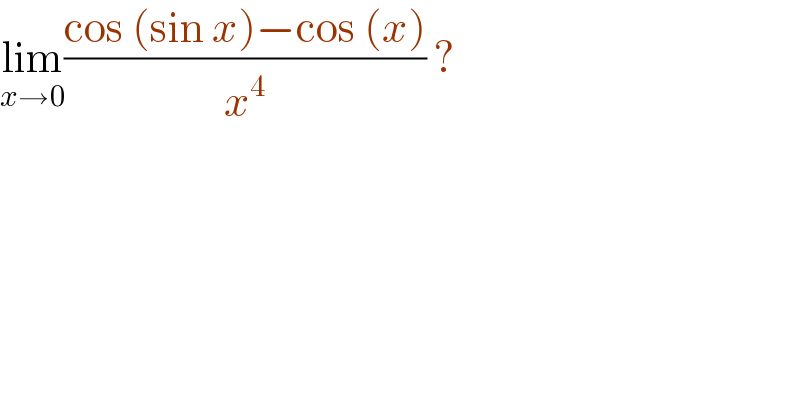
lim_(x→0) ((cos (sin x)−cos (x))/x^4 ) ?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)−\mathrm{cos}\:\left({x}\right)}{{x}^{\mathrm{4}} }\:?\: \\ $$
Answered by john santu last updated on 24/Jul/20
lim_(x→0) ((−2sin (((x+sin x)/2))sin (((sin x−x)/2)))/x^4 ) lim_(x→0) ((−2(((x+sin x)/2))(((sin x−x)/2)))/x^4 ) lim_(x→0) −(((x+x+(x^3 /(3!)))(x+(x^3 /(3!))−x))/(2x^4 )) lim_(x→0) −(((x^3 /6)(2x+(x^3 /6)))/(2x^4 )) =− lim_(x→0) ((x^4 (2+(x^2 /6)))/(12x^4 )) = −(1/6) . (JS ♠)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:\left(\frac{{x}+\mathrm{sin}\:{x}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\mathrm{sin}\:{x}−{x}}{\mathrm{2}}\right)}{{x}^{\mathrm{4}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\left(\frac{{x}+\mathrm{sin}\:{x}}{\mathrm{2}}\right)\left(\frac{\mathrm{sin}\:{x}−{x}}{\mathrm{2}}\right)}{{x}^{\mathrm{4}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\left({x}+{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−{x}\right)}{\mathrm{2}{x}^{\mathrm{4}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:−\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\left(\mathrm{2}{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{2}{x}^{\mathrm{4}} }\:=−\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{4}} \left(\mathrm{2}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)}{\mathrm{12}{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{6}}\:.\:\left({JS}\:\spadesuit\right) \\ $$
Answered by mathmax by abdo last updated on 24/Jul/20
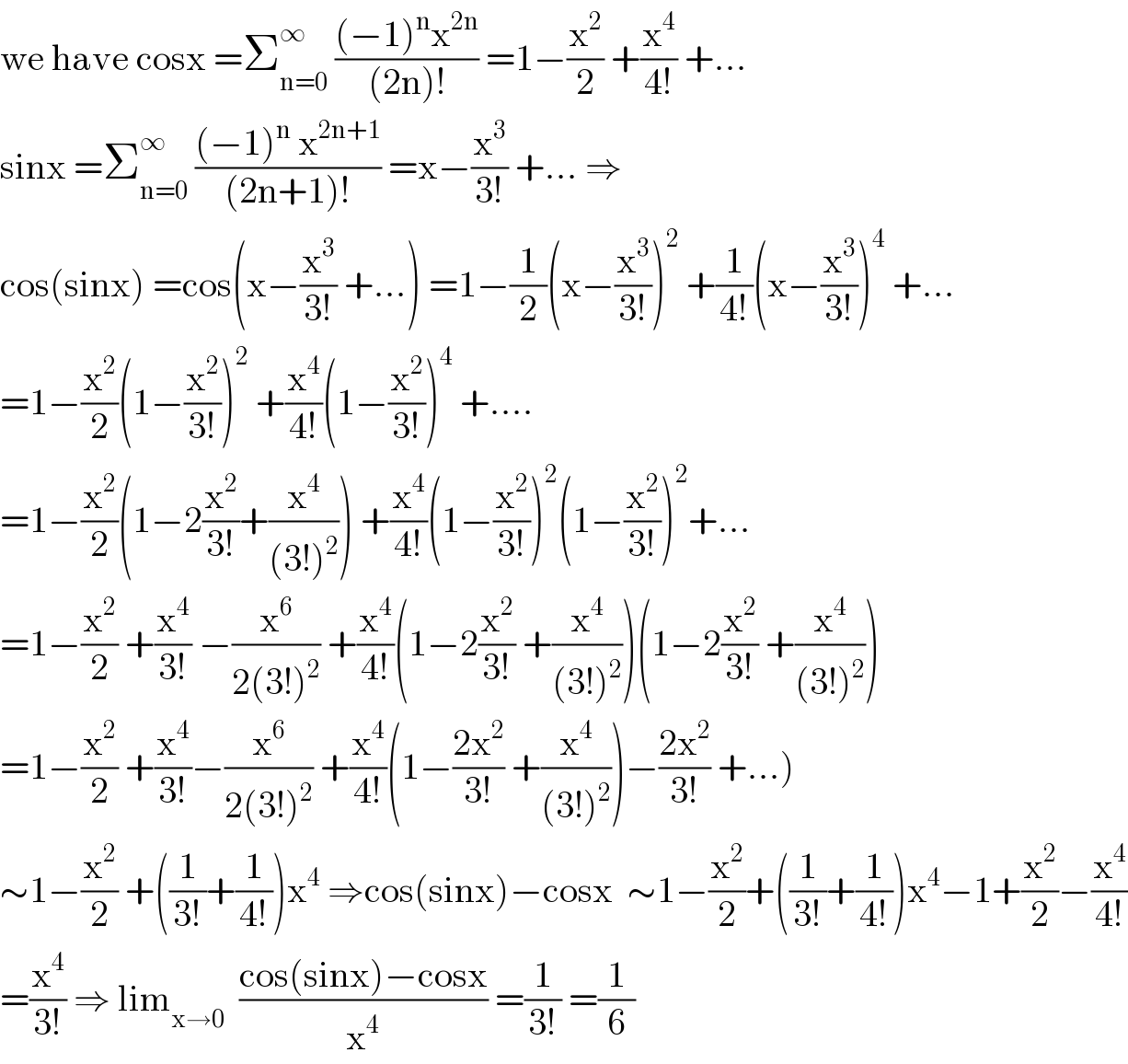
we have cosx =Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n)!)) =1−(x^2 /2) +(x^4 /(4!)) +... sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) =x−(x^3 /(3!)) +... ⇒ cos(sinx) =cos(x−(x^3 /(3!)) +...) =1−(1/2)(x−(x^3 /(3!)))^2 +(1/(4!))(x−(x^3 /(3!)))^4 +... =1−(x^2 /2)(1−(x^2 /(3!)))^2 +(x^4 /(4!))(1−(x^2 /(3!)))^4 +.... =1−(x^2 /2)(1−2(x^2 /(3!))+(x^4 /((3!)^2 ))) +(x^4 /(4!))(1−(x^2 /(3!)))^2 (1−(x^2 /(3!)))^2 +... =1−(x^2 /2) +(x^4 /(3!)) −(x^6 /(2(3!)^2 )) +(x^4 /(4!))(1−2(x^2 /(3!)) +(x^4 /((3!)^2 )))(1−2(x^2 /(3!)) +(x^4 /((3!)^2 ))) =1−(x^2 /2) +(x^4 /(3!))−(x^6 /(2(3!)^2 )) +(x^4 /(4!))(1−((2x^2 )/(3!)) +(x^4 /((3!)^2 )))−((2x^2 )/(3!)) +...) ∼1−(x^2 /2) +((1/(3!))+(1/(4!)))x^4 ⇒cos(sinx)−cosx ∼1−(x^2 /2)+((1/(3!))+(1/(4!)))x^4 −1+(x^2 /2)−(x^4 /(4!)) =(x^4 /(3!)) ⇒ lim_(x→0) ((cos(sinx)−cosx)/x^4 ) =(1/(3!)) =(1/6)
$$\mathrm{we}\:\mathrm{have}\:\mathrm{cosx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\:=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\:+… \\ $$$$\mathrm{sinx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\:+…\:\Rightarrow \\ $$$$\mathrm{cos}\left(\mathrm{sinx}\right)\:=\mathrm{cos}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\:+…\right)\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}!}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\right)^{\mathrm{4}} \:+… \\ $$$$=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}\right)^{\mathrm{2}} \:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}\right)^{\mathrm{4}} \:+…. \\ $$$$=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{\mathrm{x}^{\mathrm{4}} }{\left(\mathrm{3}!\right)^{\mathrm{2}} }\right)\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}\right)^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}\right)^{\mathrm{2}} +… \\ $$$$=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{3}!}\:−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{2}\left(\mathrm{3}!\right)^{\mathrm{2}} }\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\left(\mathrm{1}−\mathrm{2}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\left(\mathrm{3}!\right)^{\mathrm{2}} }\right)\left(\mathrm{1}−\mathrm{2}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}!}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\left(\mathrm{3}!\right)^{\mathrm{2}} }\right) \\ $$$$\left.=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{3}!}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{2}\left(\mathrm{3}!\right)^{\mathrm{2}} }\:+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\left(\mathrm{1}−\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{3}!}\:+\frac{\mathrm{x}^{\mathrm{4}} }{\left(\mathrm{3}!\right)^{\mathrm{2}} }\right)−\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{3}!}\:+…\right) \\ $$$$\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\left(\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}\right)\mathrm{x}^{\mathrm{4}} \:\Rightarrow\mathrm{cos}\left(\mathrm{sinx}\right)−\mathrm{cosx}\:\:\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\left(\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}\right)\mathrm{x}^{\mathrm{4}} −\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!} \\ $$$$=\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{3}!}\:\Rightarrow\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{cos}\left(\mathrm{sinx}\right)−\mathrm{cosx}}{\mathrm{x}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{3}!}\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *