Question Number 119902 by benjo_mathlover last updated on 28/Oct/20
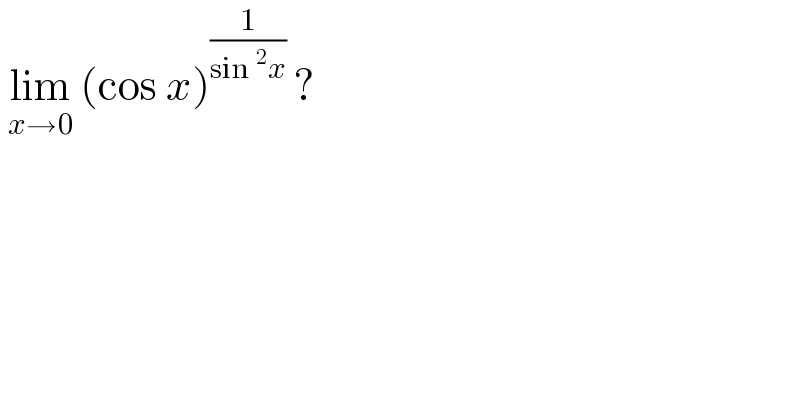
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}}} \:? \\ $$
Answered by benjo_mathlover last updated on 28/Oct/20

Answered by Olaf last updated on 28/Oct/20

$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}\mathrm{ln}\left(\mathrm{cos}{x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }×\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{cos}{x}\right)^{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}}} \:\underset{\mathrm{0}} {\sim}\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Answered by 1549442205PVT last updated on 28/Oct/20
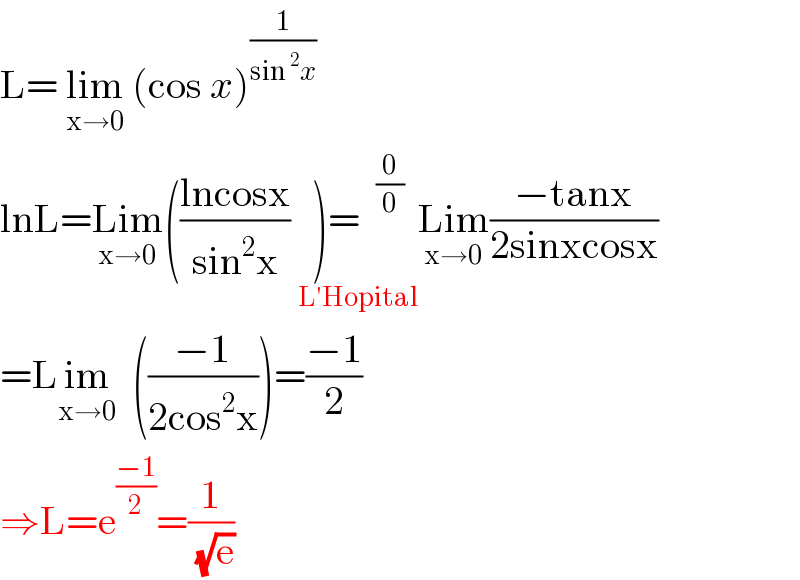
$$\mathrm{L}=\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}}} \: \\ $$$$\mathrm{lnL}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\left(\frac{\mathrm{lncosx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\:\underset{\mathrm{L}'\mathrm{Hopital}} {\right)=\:\:^{\frac{\mathrm{0}}{\mathrm{0}}} }\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{−\mathrm{tanx}}{\mathrm{2sinxcosx}} \\ $$$$=\mathrm{L}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{im}}\:\:\left(\frac{−\mathrm{1}}{\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\right)=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{L}=\mathrm{e}^{\frac{−\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}} \\ $$
