Question Number 59694 by meme last updated on 13/May/19
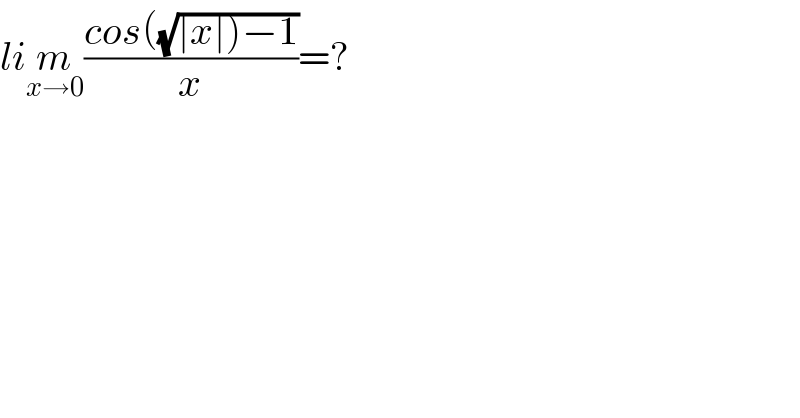
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{cos}\left(\sqrt{\left.\mid{x}\mid\right)−\mathrm{1}}\right.}{{x}}=? \\ $$
Commented by maxmathsup by imad last updated on 13/May/19
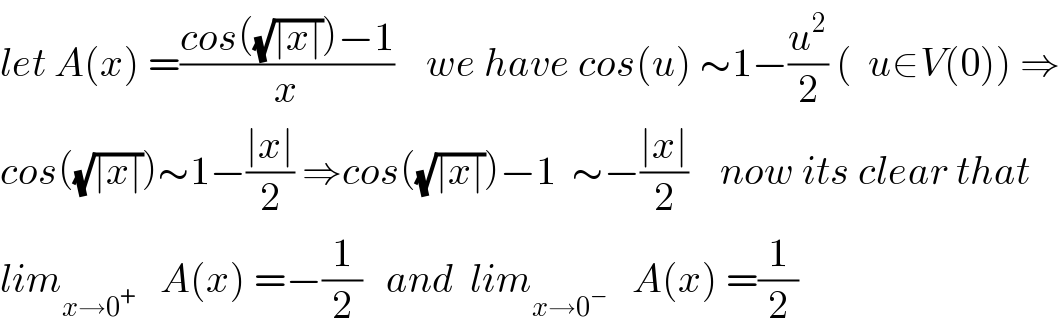
$${let}\:{A}\left({x}\right)\:=\frac{{cos}\left(\sqrt{\mid{x}\mid}\right)−\mathrm{1}}{{x}}\:\:\:\:{we}\:{have}\:{cos}\left({u}\right)\:\sim\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:\left(\:\:{u}\in{V}\left(\mathrm{0}\right)\right)\:\Rightarrow \\ $$$${cos}\left(\sqrt{\mid{x}\mid}\right)\sim\mathrm{1}−\frac{\mid{x}\mid}{\mathrm{2}}\:\Rightarrow{cos}\left(\sqrt{\mid{x}\mid}\right)−\mathrm{1}\:\:\sim−\frac{\mid{x}\mid}{\mathrm{2}}\:\:\:\:{now}\:{its}\:{clear}\:{that} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:{A}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{and}\:\:{lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:\:{A}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
