Question Number 126378 by benjo_mathlover last updated on 20/Dec/20
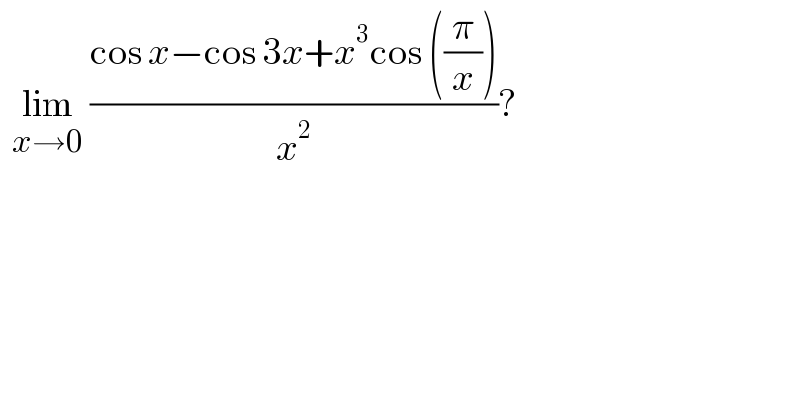
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{3}{x}+{x}^{\mathrm{3}} \mathrm{cos}\:\left(\frac{\pi}{{x}}\right)}{{x}^{\mathrm{2}} }? \\ $$
Answered by liberty last updated on 20/Dec/20
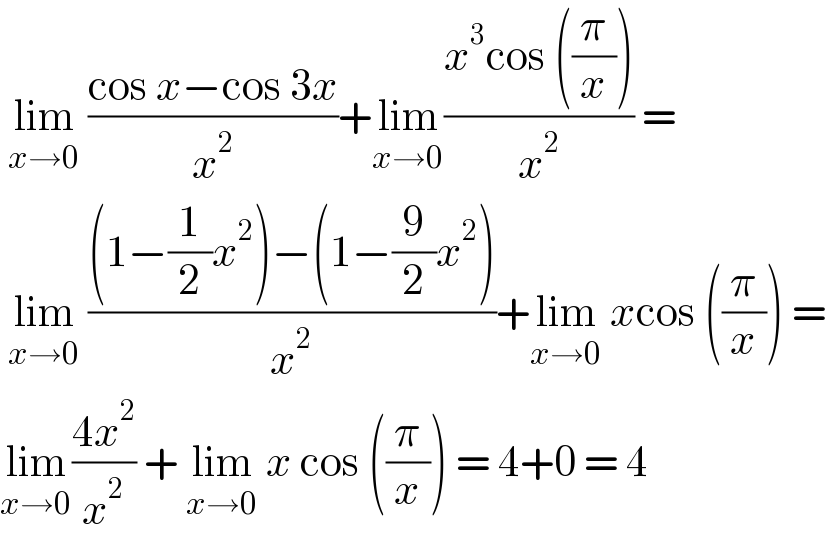
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{3}{x}}{{x}^{\mathrm{2}} }+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} \mathrm{cos}\:\left(\frac{\pi}{{x}}\right)}{{x}^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)−\left(\mathrm{1}−\frac{\mathrm{9}}{\mathrm{2}}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}\mathrm{cos}\:\left(\frac{\pi}{{x}}\right)\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:+\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}\:\mathrm{cos}\:\left(\frac{\pi}{{x}}\right)\:=\:\mathrm{4}+\mathrm{0}\:=\:\mathrm{4} \\ $$
