Question Number 117637 by bemath last updated on 13/Oct/20
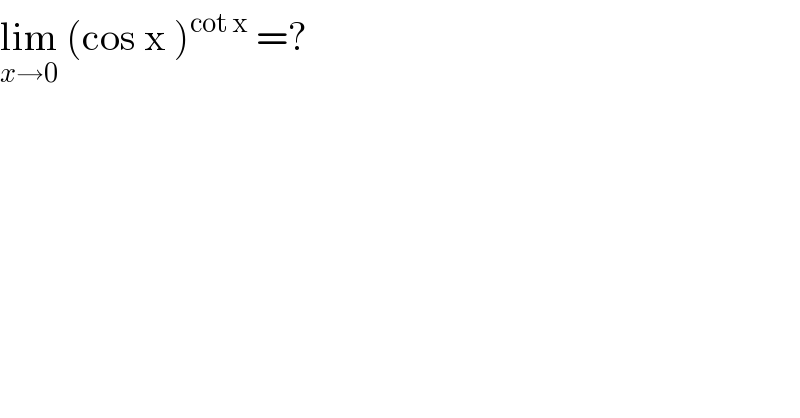
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}\:\mathrm{x}\:\right)^{\mathrm{cot}\:\mathrm{x}} \:=? \\ $$
Answered by AbduraufKodiriy last updated on 13/Oct/20
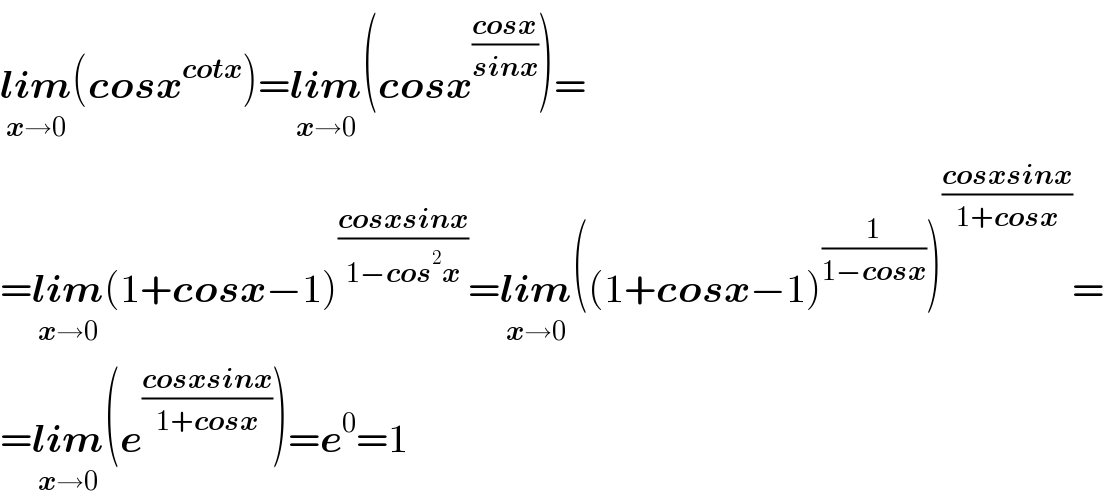
$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\left(\boldsymbol{{cosx}}^{\boldsymbol{{cotx}}} \right)=\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\left(\boldsymbol{{cosx}}^{\frac{\boldsymbol{{cosx}}}{\boldsymbol{{sinx}}}} \right)= \\ $$$$=\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\left(\mathrm{1}+\boldsymbol{{cosx}}−\mathrm{1}\right)^{\frac{\boldsymbol{{cosxsinx}}}{\mathrm{1}−\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}}}} =\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\left(\left(\mathrm{1}+\boldsymbol{{cosx}}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{1}−\boldsymbol{{cosx}}}} \right)^{\frac{\boldsymbol{{cosxsinx}}}{\mathrm{1}+\boldsymbol{{cosx}}}} = \\ $$$$=\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\left(\boldsymbol{{e}}^{\frac{\boldsymbol{{cosxsinx}}}{\mathrm{1}+\boldsymbol{{cosx}}}} \right)=\boldsymbol{{e}}^{\mathrm{0}} =\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Oct/20
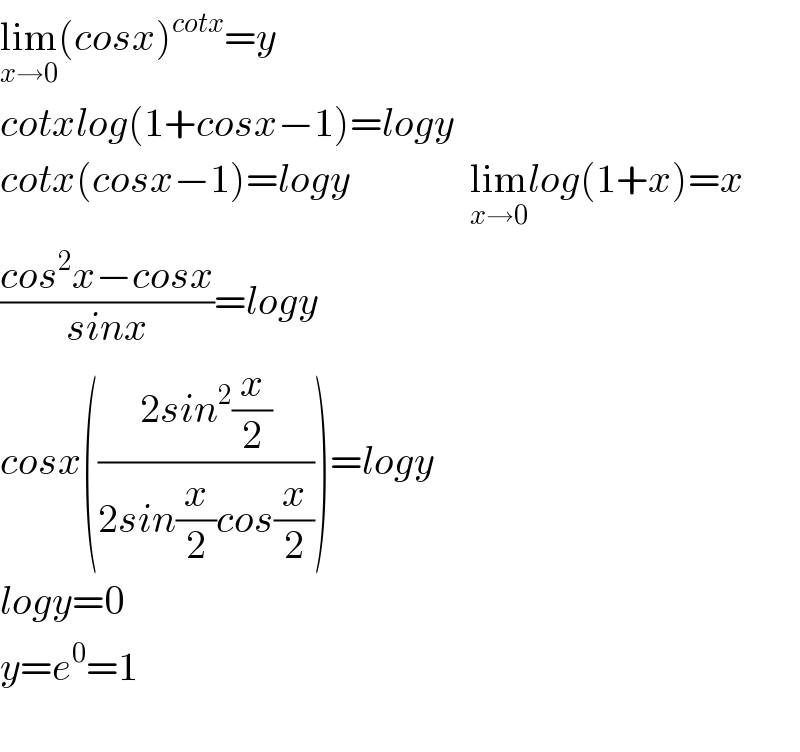
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({cosx}\right)^{{cotx}} ={y} \\ $$$${cotxlog}\left(\mathrm{1}+{cosx}−\mathrm{1}\right)={logy} \\ $$$${cotx}\left({cosx}−\mathrm{1}\right)={logy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{log}\left(\mathrm{1}+{x}\right)={x} \\ $$$$\frac{{cos}^{\mathrm{2}} {x}−{cosx}}{{sinx}}={logy} \\ $$$${cosx}\left(\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}}\right)={logy} \\ $$$${logy}=\mathrm{0} \\ $$$${y}={e}^{\mathrm{0}} =\mathrm{1} \\ $$$$ \\ $$
