Question Number 175217 by mnjuly1970 last updated on 23/Aug/22
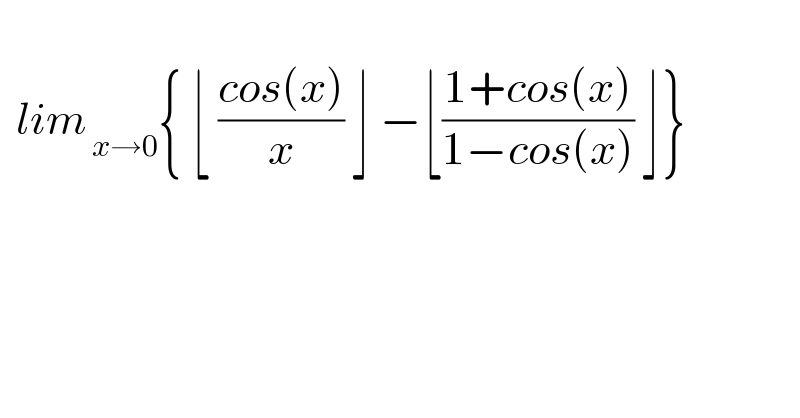
$$ \\ $$$$\:\:{lim}_{\:{x}\rightarrow\mathrm{0}} \left\{\:\lfloor\:\frac{{cos}\left({x}\right)}{{x}}\:\rfloor\:−\lfloor\frac{\mathrm{1}+{cos}\left({x}\right)}{\mathrm{1}−{cos}\left({x}\right)}\:\rfloor\right\} \\ $$
Commented by kaivan.ahmadi last updated on 24/Aug/22
![we know that [x]_(x→∞) ∼x so lim_(x→0) ((cosx)/x)−((1+cosx)/(1−cosx))= lim_(x→0) ((cosx(1−cosx)−x(1+cosx))/(x(1−cosx))) =lim_(x→0) (((1−(x^2 /2))((x^2 /2))−x(2−(x^2 /2)))/(x((x^2 /2)))) =lim_(x→0) ((−2x)/(x^3 /3))=−∞](https://www.tinkutara.com/question/Q175227.png)
$${we}\:{know}\:{that}\:\left[{x}\right]_{{x}\rightarrow\infty} \sim{x}\:{so} \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{cosx}}{{x}}−\frac{\mathrm{1}+{cosx}}{\mathrm{1}−{cosx}}= \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{cosx}\left(\mathrm{1}−{cosx}\right)−{x}\left(\mathrm{1}+{cosx}\right)}{{x}\left(\mathrm{1}−{cosx}\right)} \\ $$$$={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)−{x}\left(\mathrm{2}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{{x}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)} \\ $$$$={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{−\mathrm{2}{x}}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}=−\infty \\ $$
