Menu Close

lim-x-0-cosx-1-m-cosx-1-n-x-2-where-m-and-n-integer-

Tinku Tara 0 Comments
Pin




Question Number 82761 by TANMAY PANACEA last updated on 24/Feb/20
lim_(x→0) (((cosx)^(1/m) −(cosx)^(1/n) )/x^2 ) [where m and n integer]
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} }\:\:\left[{where}\:{m}\:{and}\:{n}\:{integer}\right] \\ $$
Commented by mr W last updated on 24/Feb/20
lim_(x→0) (((cosx)^(1/m) −(cosx)^(1/n) )/x^2 ) =lim_(x→0) (((1−2 sin^2 (x/2))^(1/m) −(1−2 sin^2 (x/2))^(1/n) )/x^2 ) =lim_(x→0) ((1−(2/m) sin^2 (x/2)+o(sin^2 (x/2))−[1−(2/n) sin^2 (x/2)+o(sin^2 (x/2))])/x^2 ) =lim_(x→0) ((2((1/n)−(1/m)) sin^2 (x/2))/x^2 ) =(1/2)((1/n)−(1/m))lim_(x→0) ((( sin (x/2))/(x/2)))^2 =(1/2)((1/n)−(1/m))
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{m}}} −\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{2}}{{m}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}+{o}\left(\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)−\left[\mathrm{1}−\frac{\mathrm{2}}{{n}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}+{o}\left(\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)\right]}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{m}}\right)\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{m}}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}{\frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{m}}\right) \\ $$
Commented by TANMAY PANACEA last updated on 24/Feb/20
excellent sir...
$${excellent}\:{sir}… \\ $$
Commented by jagoll last updated on 24/Feb/20
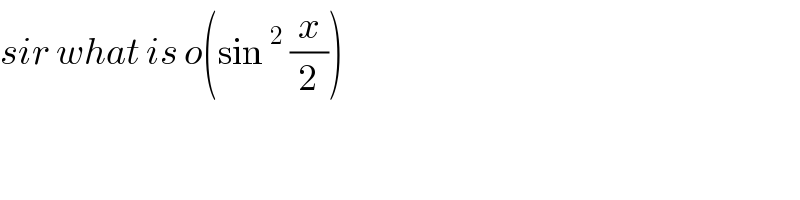
sir what is o(sin^2 (x/2))
$${sir}\:{what}\:{is}\:{o}\left(\mathrm{sin}\:^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right) \\ $$
Commented by abdomathmax last updated on 24/Feb/20
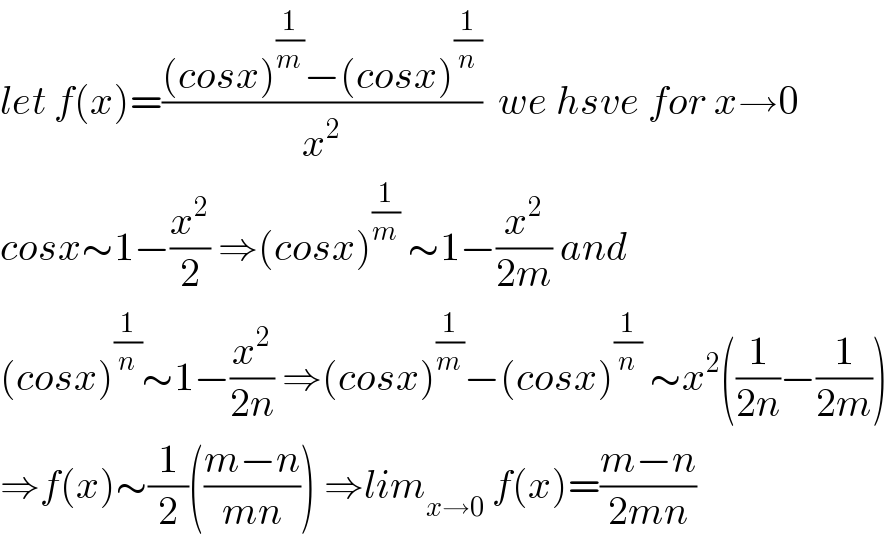
let f(x)=(((cosx)^(1/m) −(cosx)^(1/n) )/x^2 ) we hsve for x→0 cosx∼1−(x^2 /2) ⇒(cosx)^(1/m) ∼1−(x^2 /(2m)) and (cosx)^(1/n) ∼1−(x^2 /(2n)) ⇒(cosx)^(1/m) −(cosx)^(1/n) ∼x^2 ((1/(2n))−(1/(2m))) ⇒f(x)∼(1/2)(((m−n)/(mn))) ⇒lim_(x→0) f(x)=((m−n)/(2mn))
$${let}\:{f}\left({x}\right)=\frac{\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} }\:\:{we}\:{hsve}\:{for}\:{x}\rightarrow\mathrm{0} \\ $$$${cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} \:\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{m}}\:{and} \\ $$$$\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} \sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{n}}\:\Rightarrow\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} \:\sim{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{m}}\right) \\ $$$$\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{m}−{n}}{{mn}}\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right)=\frac{{m}−{n}}{\mathrm{2}{mn}} \\ $$
Commented by mr W last updated on 24/Feb/20
to jagoll sir: o(x^2 ) stands for terms with higher orders than x^2 . for example: cos x=1−(x^2 /(2!))+(x^4 /(4!))−(x^6 /(6!))+...... =1−(x^2 /(2!))+(x^4 /(4!))+o(x^4 ) =1−(x^2 /(2!))+o(x^2 ) search in google for “little o notation” for more.
$${to}\:{jagoll}\:{sir}: \\ $$$${o}\left({x}^{\mathrm{2}} \right)\:{stands}\:{for}\:{terms}\:{with}\:{higher}\:{orders} \\ $$$${than}\:{x}^{\mathrm{2}} .\:{for}\:{example}: \\ $$$$\mathrm{cos}\:{x}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+…… \\ $$$$=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$$=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$${search}\:{in}\:{google}\:{for}\:“{little}\:{o}\:{notation}'' \\ $$$${for}\:{more}. \\ $$
Commented by jagoll last updated on 24/Feb/20
thank you . sir
$${thank}\:{you}\:.\:{sir}\: \\ $$
Commented by mathmax by abdo last updated on 24/Feb/20
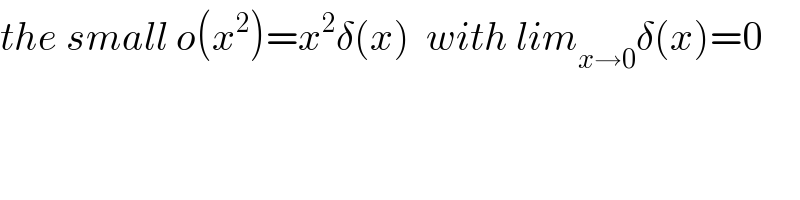
the small o(x^2 )=x^2 δ(x) with lim_(x→0) δ(x)=0
$${the}\:{small}\:{o}\left({x}^{\mathrm{2}} \right)={x}^{\mathrm{2}} \delta\left({x}\right)\:\:{with}\:{lim}_{{x}\rightarrow\mathrm{0}} \delta\left({x}\right)=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *