Question Number 127213 by Study last updated on 27/Dec/20
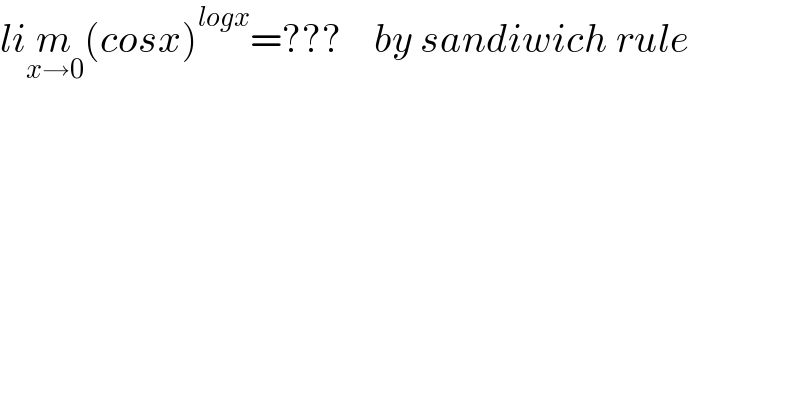
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left({cosx}\right)^{{logx}} =???\:\:\:\:{by}\:{sandiwich}\:{rule} \\ $$
Commented by Study last updated on 27/Dec/20

$${help}\:{me} \\ $$
Commented by Study last updated on 28/Dec/20
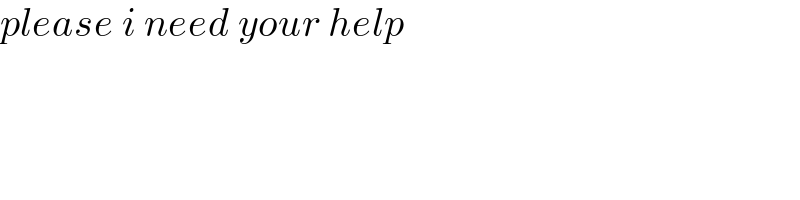
$${please}\:{i}\:{need}\:{your}\:{help} \\ $$
Answered by mathmax by abdo last updated on 28/Dec/20
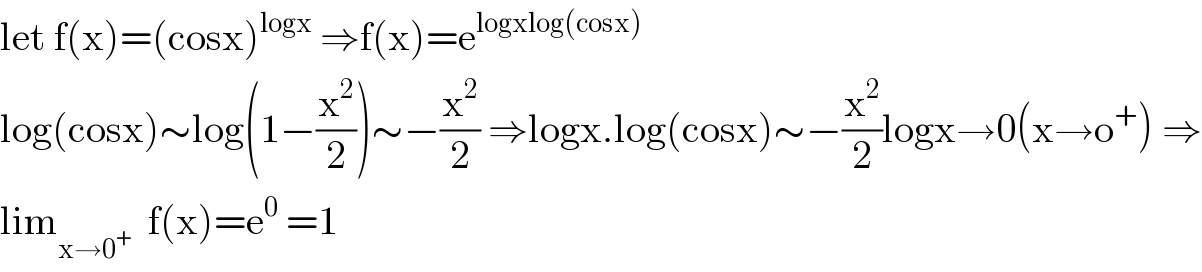
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{cosx}\right)^{\mathrm{logx}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{logxlog}\left(\mathrm{cosx}\right)} \\ $$$$\mathrm{log}\left(\mathrm{cosx}\right)\sim\mathrm{log}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{logx}.\mathrm{log}\left(\mathrm{cosx}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{logx}\rightarrow\mathrm{0}\left(\mathrm{x}\rightarrow\mathrm{o}^{+} \right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$
Commented by Study last updated on 28/Dec/20
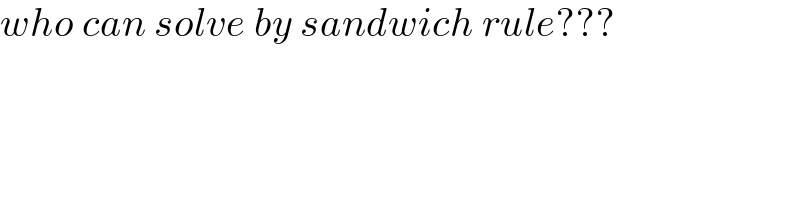
$${who}\:{can}\:{solve}\:{by}\:{sandwich}\:{rule}??? \\ $$
