Menu Close

lim-x-0-cot-x-1-ln-x-

Tinku Tara 0 Comments
Pin




Question Number 121460 by bramlexs22 last updated on 08/Nov/20
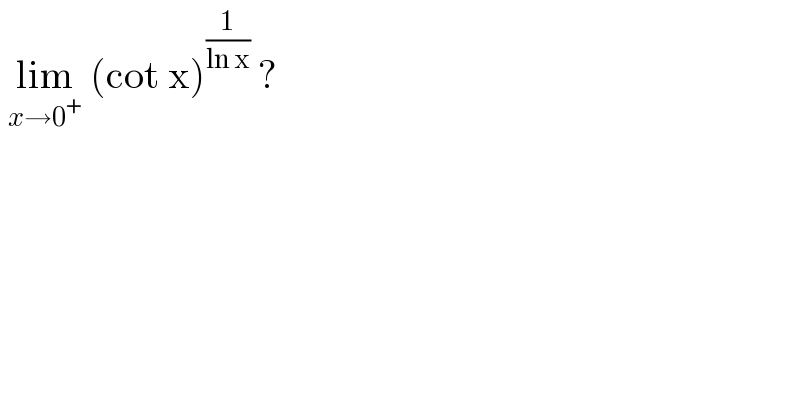
lim_(x→0^+ ) (cot x)^(1/(ln x)) ?
limx→0+(cotx)1lnx?
Answered by Dwaipayan Shikari last updated on 08/Nov/20
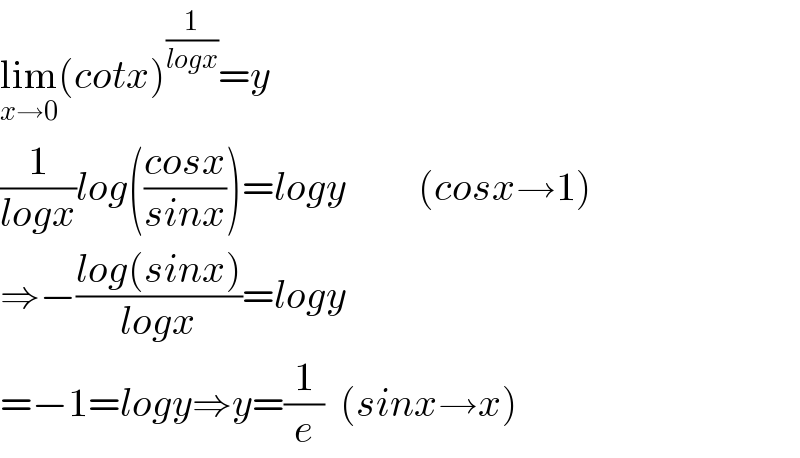
lim_(x→0) (cotx)^(1/(logx)) =y (1/(logx))log(((cosx)/(sinx)))=logy (cosx→1) ⇒−((log(sinx))/(logx))=logy =−1=logy⇒y=(1/e) (sinx→x)
limx→0(cotx)1logx=y1logxlog(cosxsinx)=logy(cosx→1)⇒−log(sinx)logx=logy=−1=logy⇒y=1e(sinx→x)
Answered by liberty last updated on 08/Nov/20
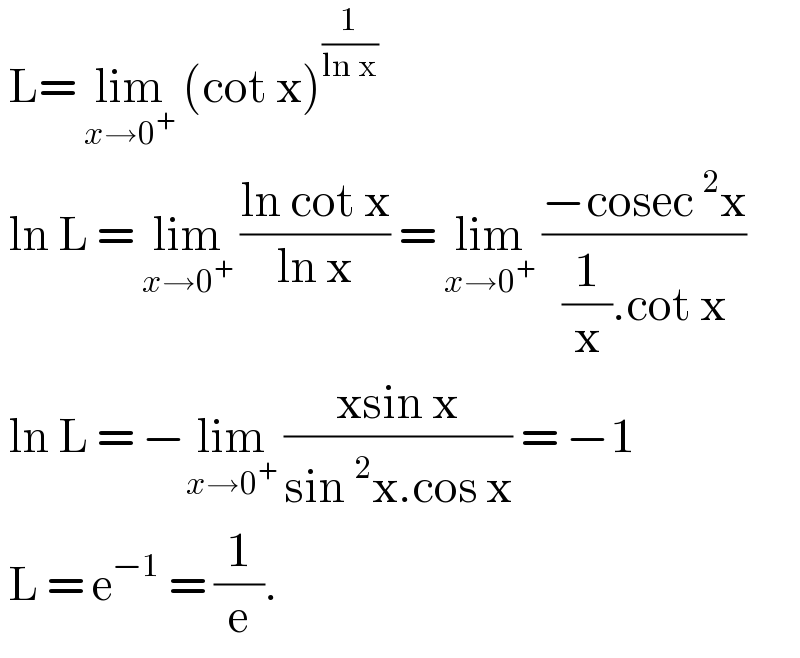
L= lim_(x→0^+ ) (cot x)^(1/(ln x)) ln L = lim_(x→0^+ ) ((ln cot x)/(ln x)) = lim_(x→0^+ ) ((−cosec^2 x)/((1/x).cot x)) ln L = −lim_(x→0^+ ) ((xsin x)/(sin^2 x.cos x)) = −1 L = e^(−1) = (1/e).
L=limx→0+(cotx)1lnxlnL=limx→0+lncotxlnx=limx→0+−cosec2x1x.cotxlnL=−limx→0+xsinxsin2x.cosx=−1L=e−1=1e.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *