Question Number 116019 by bemath last updated on 30/Sep/20
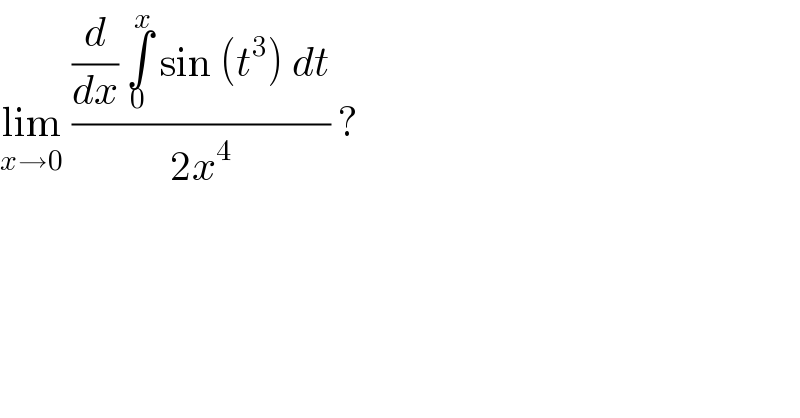
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\mathrm{sin}\:\left({t}^{\mathrm{3}} \right)\:{dt}}{\mathrm{2}{x}^{\mathrm{4}} }\:? \\ $$
Commented by bemath last updated on 30/Sep/20
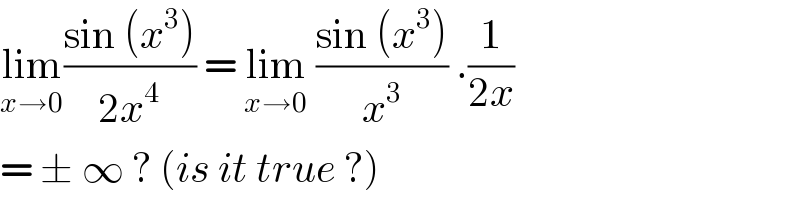
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left({x}^{\mathrm{3}} \right)}{\mathrm{2}{x}^{\mathrm{4}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left({x}^{\mathrm{3}} \right)}{{x}^{\mathrm{3}} }\:.\frac{\mathrm{1}}{\mathrm{2}{x}} \\ $$$$=\:\pm\:\infty\:?\:\left({is}\:{it}\:{true}\:?\right) \\ $$
Commented by MJS_new last updated on 30/Sep/20
![lim_(x→0) (((d/dx)[∫_0 ^x sin (t^3 ) dt])/(2x^4 )) =lim_(x→0) ((sin x^3 )/(2x^4 )) = =lim_(x→0) ((3cos x^3 )/(8x)) doesn′t exist](https://www.tinkutara.com/question/Q116027.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left[\underset{\mathrm{0}} {\overset{{x}} {\int}}\mathrm{sin}\:\left({t}^{\mathrm{3}} \right)\:{dt}\right]}{\mathrm{2}{x}^{\mathrm{4}} }\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}^{\mathrm{3}} }{\mathrm{2}{x}^{\mathrm{4}} }\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3cos}\:{x}^{\mathrm{3}} }{\mathrm{8}{x}}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$
Commented by bemath last updated on 30/Sep/20

$${thank}\:{you}\:{sir}\:{for}\:{your}\:{correction} \\ $$
