Question Number 83329 by john santu last updated on 01/Mar/20
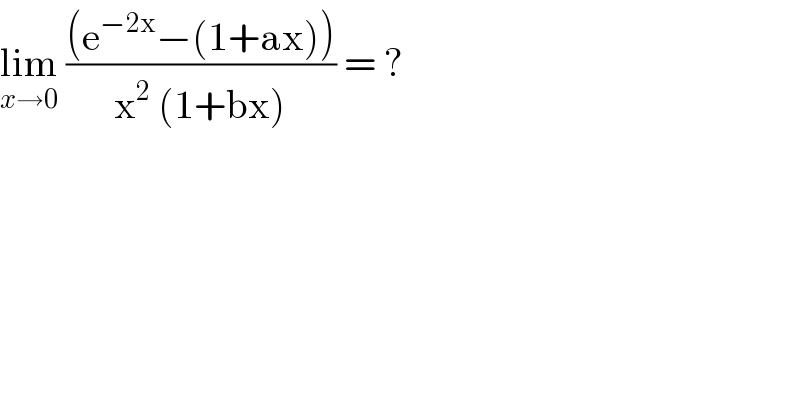
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{e}^{−\mathrm{2x}} −\left(\mathrm{1}+\mathrm{ax}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:\left(\mathrm{1}+\mathrm{bx}\right)}\:=\:? \\ $$
Commented by jagoll last updated on 01/Mar/20
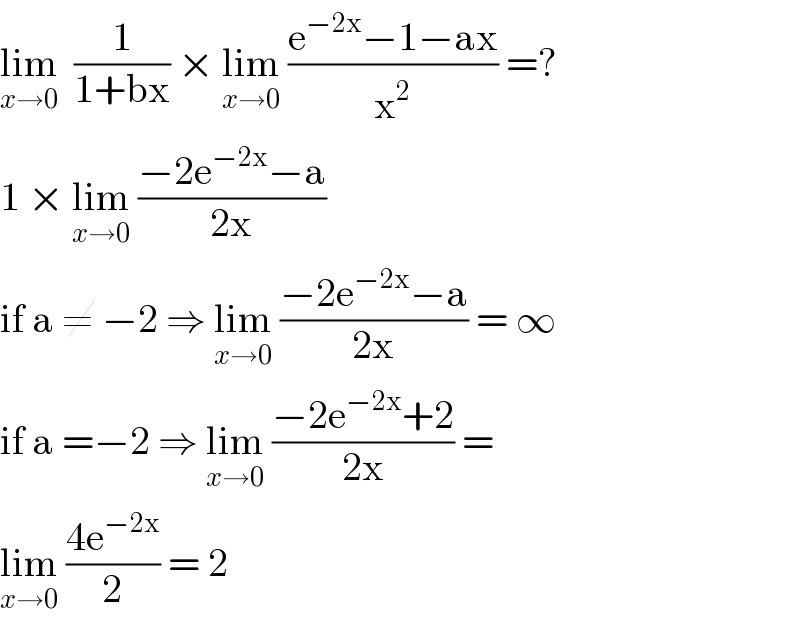
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{bx}}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{−\mathrm{2x}} −\mathrm{1}−\mathrm{ax}}{\mathrm{x}^{\mathrm{2}} }\:=? \\ $$$$\mathrm{1}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2e}^{−\mathrm{2x}} −\mathrm{a}}{\mathrm{2x}}\: \\ $$$$\mathrm{if}\:\mathrm{a}\:\neq\:−\mathrm{2}\:\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2e}^{−\mathrm{2x}} −\mathrm{a}}{\mathrm{2x}}\:=\:\infty \\ $$$$\mathrm{if}\:\mathrm{a}\:=−\mathrm{2}\:\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2e}^{−\mathrm{2x}} +\mathrm{2}}{\mathrm{2x}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4e}^{−\mathrm{2x}} }{\mathrm{2}}\:=\:\mathrm{2} \\ $$
Answered by jagoll last updated on 01/Mar/20
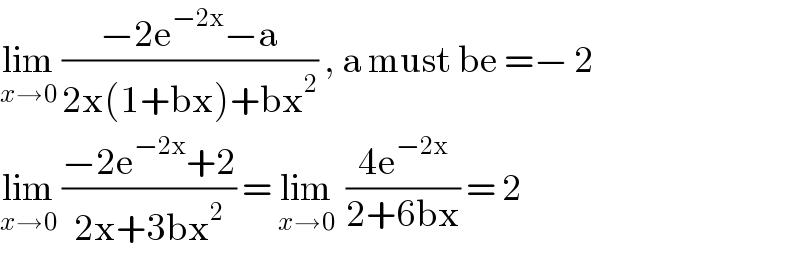
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2e}^{−\mathrm{2x}} −\mathrm{a}}{\mathrm{2x}\left(\mathrm{1}+\mathrm{bx}\right)+\mathrm{bx}^{\mathrm{2}} }\:,\:\mathrm{a}\:\mathrm{must}\:\mathrm{be}\:=−\:\mathrm{2} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2e}^{−\mathrm{2x}} +\mathrm{2}}{\mathrm{2x}+\mathrm{3bx}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{4e}^{−\mathrm{2x}} }{\mathrm{2}+\mathrm{6bx}}\:=\:\mathrm{2} \\ $$
