Question Number 130422 by john_santu last updated on 25/Jan/21
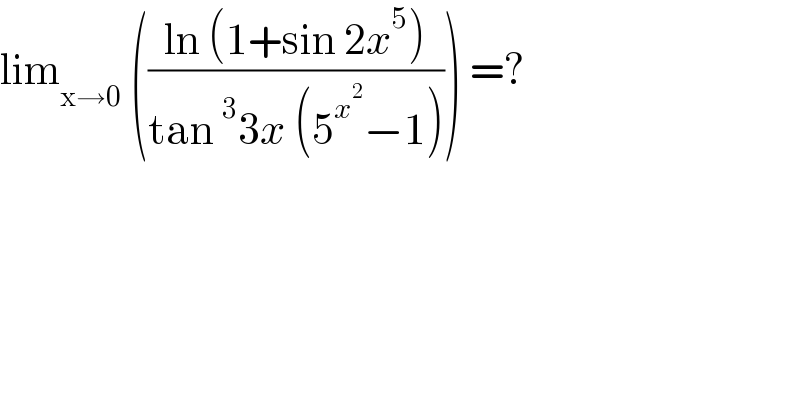
$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\left(\frac{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}^{\mathrm{5}} \right)}{\mathrm{tan}\:^{\mathrm{3}} \mathrm{3}{x}\:\left(\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{1}\right)}\right)\:=? \\ $$
Answered by liberty last updated on 25/Jan/21
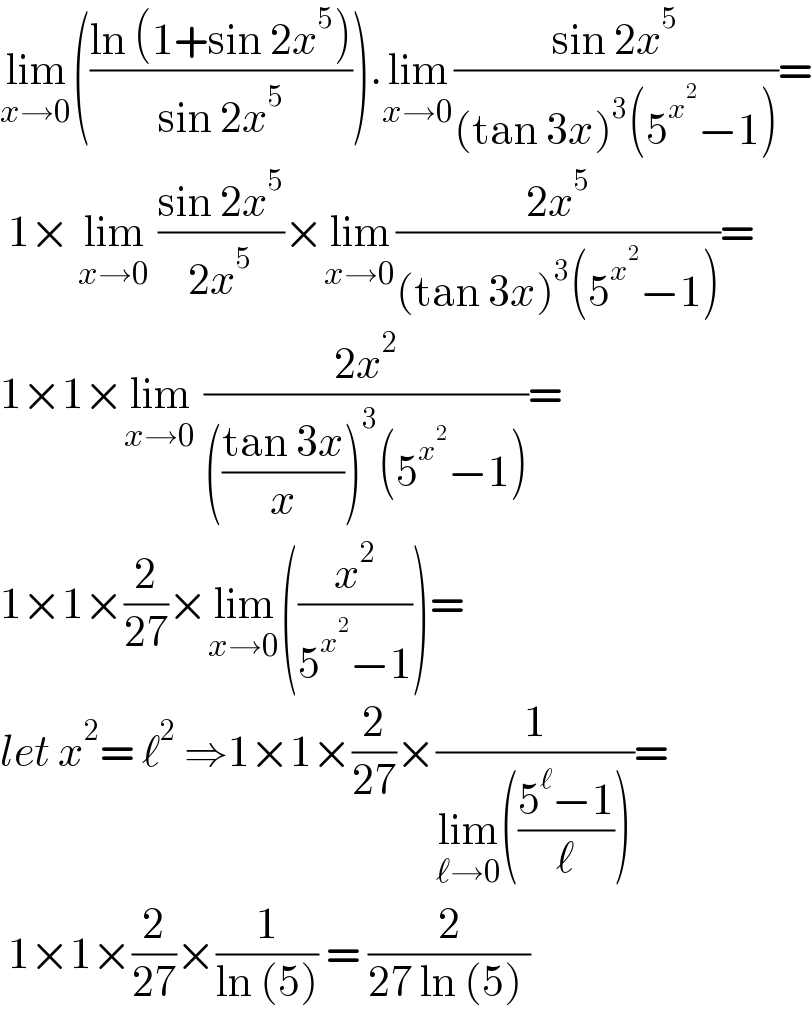
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}^{\mathrm{5}} \right)}{\mathrm{sin}\:\mathrm{2}{x}^{\mathrm{5}} }\right).\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{2}{x}^{\mathrm{5}} }{\left(\mathrm{tan}\:\mathrm{3}{x}\right)^{\mathrm{3}} \left(\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{1}\right)}= \\ $$$$\:\mathrm{1}×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{2}{x}^{\mathrm{5}} }×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{x}^{\mathrm{5}} }{\left(\mathrm{tan}\:\mathrm{3}{x}\right)^{\mathrm{3}} \left(\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{1}\right)}= \\ $$$$\mathrm{1}×\mathrm{1}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\frac{\mathrm{tan}\:\mathrm{3}{x}}{{x}}\right)^{\mathrm{3}} \left(\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{1}\right)}= \\ $$$$\mathrm{1}×\mathrm{1}×\frac{\mathrm{2}}{\mathrm{27}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{1}}\right)= \\ $$$${let}\:{x}^{\mathrm{2}} =\:\ell^{\mathrm{2}} \:\Rightarrow\mathrm{1}×\mathrm{1}×\frac{\mathrm{2}}{\mathrm{27}}×\frac{\mathrm{1}}{\underset{\ell\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{5}^{\ell} −\mathrm{1}}{\ell}\right)}= \\ $$$$\:\mathrm{1}×\mathrm{1}×\frac{\mathrm{2}}{\mathrm{27}}×\frac{\mathrm{1}}{\mathrm{ln}\:\left(\mathrm{5}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{27}\:\mathrm{ln}\:\left(\mathrm{5}\right)\:} \\ $$
