Question Number 184878 by mathlove last updated on 13/Jan/23

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}\left(\mathrm{1}+{sinx}\right)}{{sinx}}=? \\ $$$${with}\:{out}\:{H}'{L}\:{Roule} \\ $$
Answered by aba last updated on 13/Jan/23
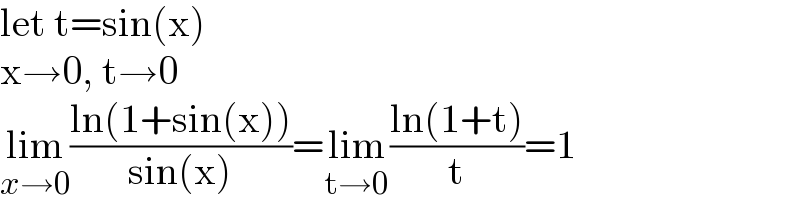
$$\mathrm{let}\:\mathrm{t}=\mathrm{sin}\left(\mathrm{x}\right) \\ $$$$\mathrm{x}\rightarrow\mathrm{0},\:\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\left(\mathrm{x}\right)\right)}{\mathrm{sin}\left(\mathrm{x}\right)}=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{t}}=\mathrm{1} \\ $$
Commented by mathlove last updated on 13/Jan/23

$${thanks}\:{a}\:{lot}\:{sir} \\ $$
