Question Number 125649 by bramlexs22 last updated on 12/Dec/20
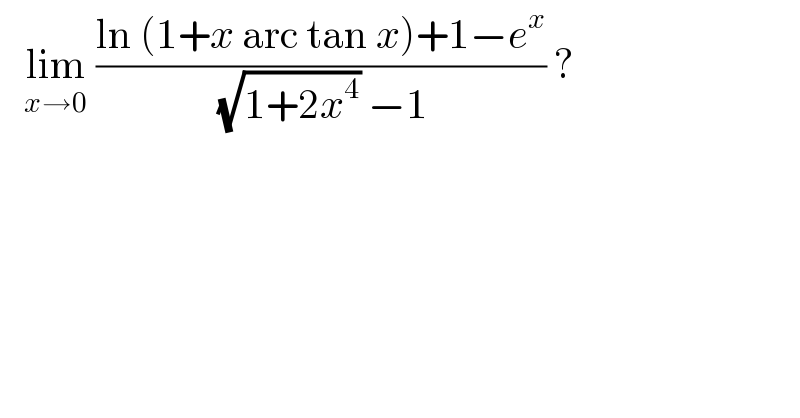
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\:\mathrm{arc}\:\mathrm{tan}\:{x}\right)+\mathrm{1}−{e}^{{x}} }{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{4}} }\:−\mathrm{1}}\:?\: \\ $$
Answered by Olaf last updated on 13/Dec/20

$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{ln}\left(\mathrm{1}+{x}\mathrm{arctan}{x}\right)+\mathrm{1}−{e}^{{x}} }{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{4}} }−\mathrm{1}} \\ $$$${f}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{ln}\left(\mathrm{1}+{x}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)\right)+\mathrm{1}−{e}^{{x}} }{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{4}} }−\mathrm{1}} \\ $$$${f}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\left({x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{3}}\right)+\mathrm{1}−\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\:\left(\mathrm{1}+{x}^{\mathrm{4}} \right)−\mathrm{1}} \\ $$$${f}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −{x}}{\:{x}^{\mathrm{4}} }\:\rightarrow\:\infty \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 13/Dec/20
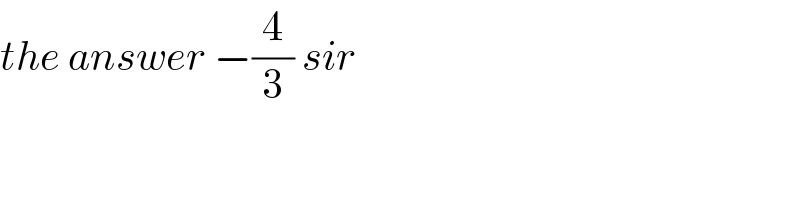
$${the}\:{answer}\:−\frac{\mathrm{4}}{\mathrm{3}}\:{sir} \\ $$
