Menu Close

lim-x-0-ln-cosh-x-ln-cos-x-2-cosh-x-cos-x-2-

Tinku Tara 0 Comments
Pin




Question Number 117687 by bemath last updated on 13/Oct/20
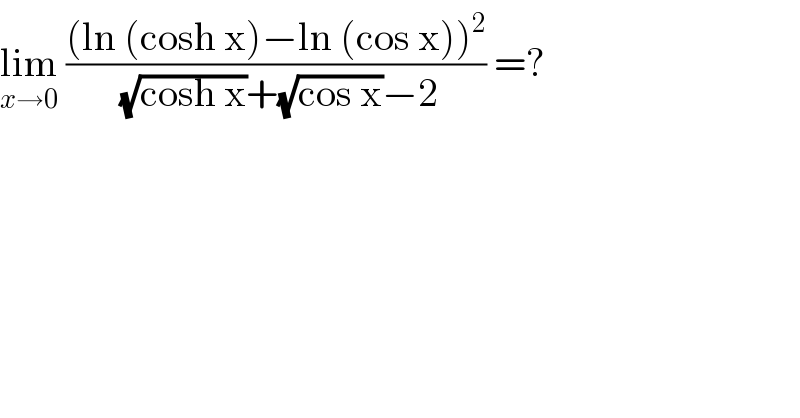
lim_(x→0) (((ln (cosh x)−ln (cos x))^2 )/( (√(cosh x))+(√(cos x))−2)) =?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{ln}\:\left(\mathrm{cosh}\:\mathrm{x}\right)−\mathrm{ln}\:\left(\mathrm{cos}\:\mathrm{x}\right)\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{cosh}\:\mathrm{x}}+\sqrt{\mathrm{cos}\:\mathrm{x}}−\mathrm{2}}\:=?\: \\ $$
Answered by 1549442205PVT last updated on 13/Oct/20
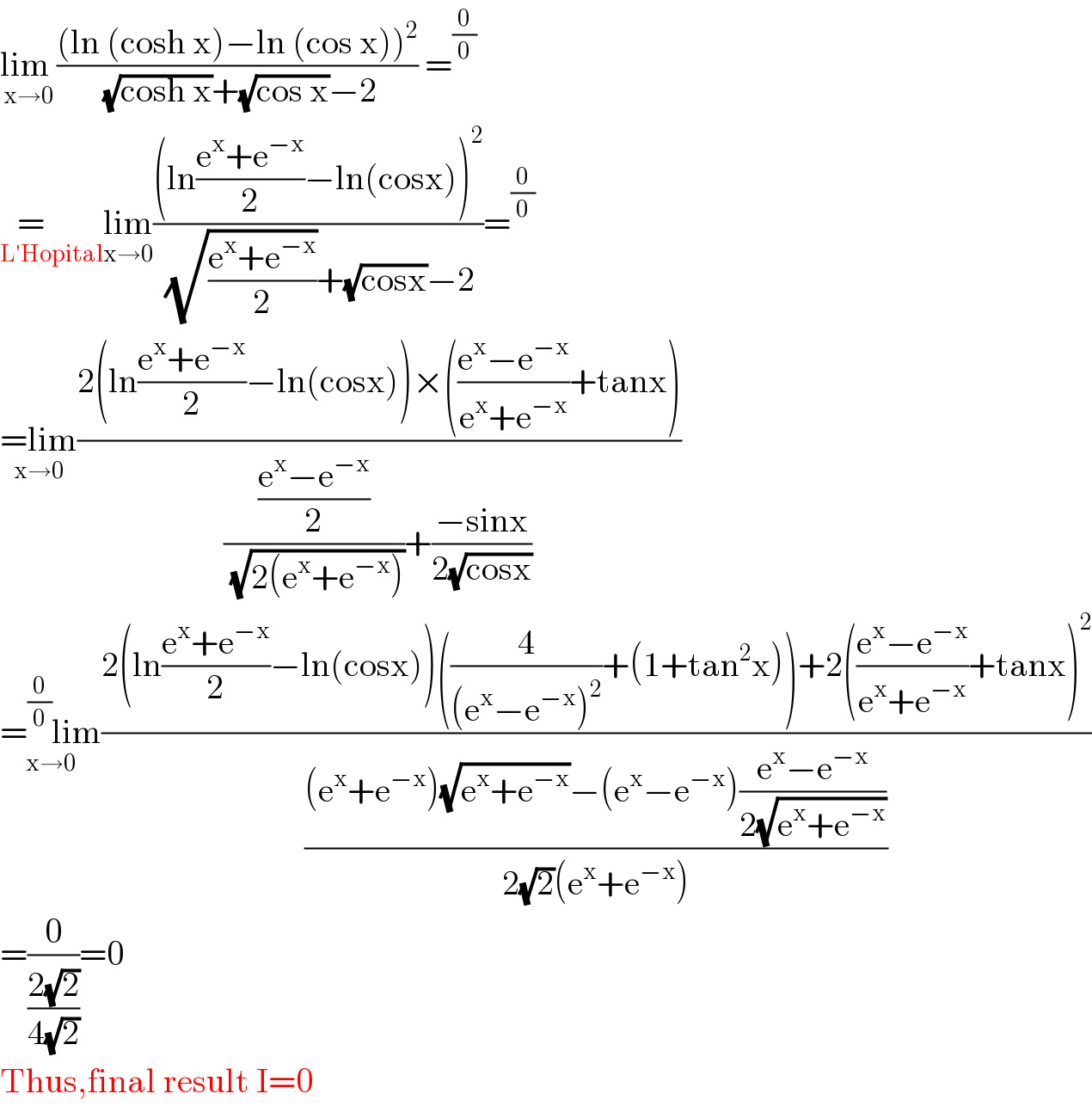
lim _(x→0) (((ln (cosh x)−ln (cos x))^2 )/( (√(cosh x))+(√(cos x))−2)) =^(0/0) = _(L′Hopital) lim_(x→0) (((ln((e^x +e^(−x) )/2)−ln(cosx))^2 )/( (√((e^x +e^(−x) )/2))+(√(cosx))−2))=^(0/0) =lim_(x→0) ((2(ln((e^x +e^(−x) )/2)−ln(cosx))×(((e^x −e^(−x) )/(e^x +e^(−x) ))+tanx))/((((e^x −e^(−x) )/2)/( (√(2(e^x +e^(−x) )))))+((−sinx)/(2(√(cosx)))))) =^(0/0) lim_(x→0) ((2(ln((e^x +e^(−x) )/2)−ln(cosx))((4/((e^x −e^(−x) )^2 ))+(1+tan^2 x))+2(((e^x −e^(−x) )/(e^x +e^(−x) ))+tanx)^2 )/(((e^x +e^(−x) )(√(e^x +e^(−x) ))−(e^x −e^(−x) )((e^x −e^(−x) )/(2(√(e^x +e^(−x) )))))/(2(√2)(e^x +e^(−x) )))) =(0/((2(√2))/(4(√2))))=0 Thus,final result I=0
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}\:}\frac{\left(\mathrm{ln}\:\left(\mathrm{cosh}\:\mathrm{x}\right)−\mathrm{ln}\:\left(\mathrm{cos}\:\mathrm{x}\right)\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{cosh}\:\mathrm{x}}+\sqrt{\mathrm{cos}\:\mathrm{x}}−\mathrm{2}}\:=^{\frac{\mathrm{0}}{\mathrm{0}}} \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}} {=\:\:\:\:\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{ln}\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}−\mathrm{ln}\left(\mathrm{cosx}\right)\right)^{\mathrm{2}} }{\:\sqrt{\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}}+\sqrt{\mathrm{cosx}}−\mathrm{2}}=^{\frac{\mathrm{0}}{\mathrm{0}}} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {=\mathrm{lim}}\frac{\mathrm{2}\left(\mathrm{ln}\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}−\mathrm{ln}\left(\mathrm{cosx}\right)\right)×\left(\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }+\mathrm{tanx}\right)}{\frac{\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}}{\:\sqrt{\mathrm{2}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} \right)}}+\frac{−\mathrm{sinx}}{\mathrm{2}\sqrt{\mathrm{cosx}}}} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {=^{\frac{\mathrm{0}}{\mathrm{0}}} \mathrm{lim}}\frac{\mathrm{2}\left(\mathrm{ln}\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}−\mathrm{ln}\left(\mathrm{cosx}\right)\right)\left(\frac{\mathrm{4}}{\left(\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} \right)^{\mathrm{2}} }+\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\right)+\mathrm{2}\left(\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }+\mathrm{tanx}\right)^{\mathrm{2}} }{\frac{\left(\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} \right)\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }−\left(\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} \right)\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }}}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} \right)}} \\ $$$$=\frac{\mathrm{0}}{\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{2}}}}=\mathrm{0} \\ $$$$\mathrm{Thus},\mathrm{final}\:\mathrm{result}\:\mathrm{I}=\mathrm{0} \\ $$
Commented by bemath last updated on 13/Oct/20
gave kudos
$$\mathrm{gave}\:\mathrm{kudos} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Oct/20
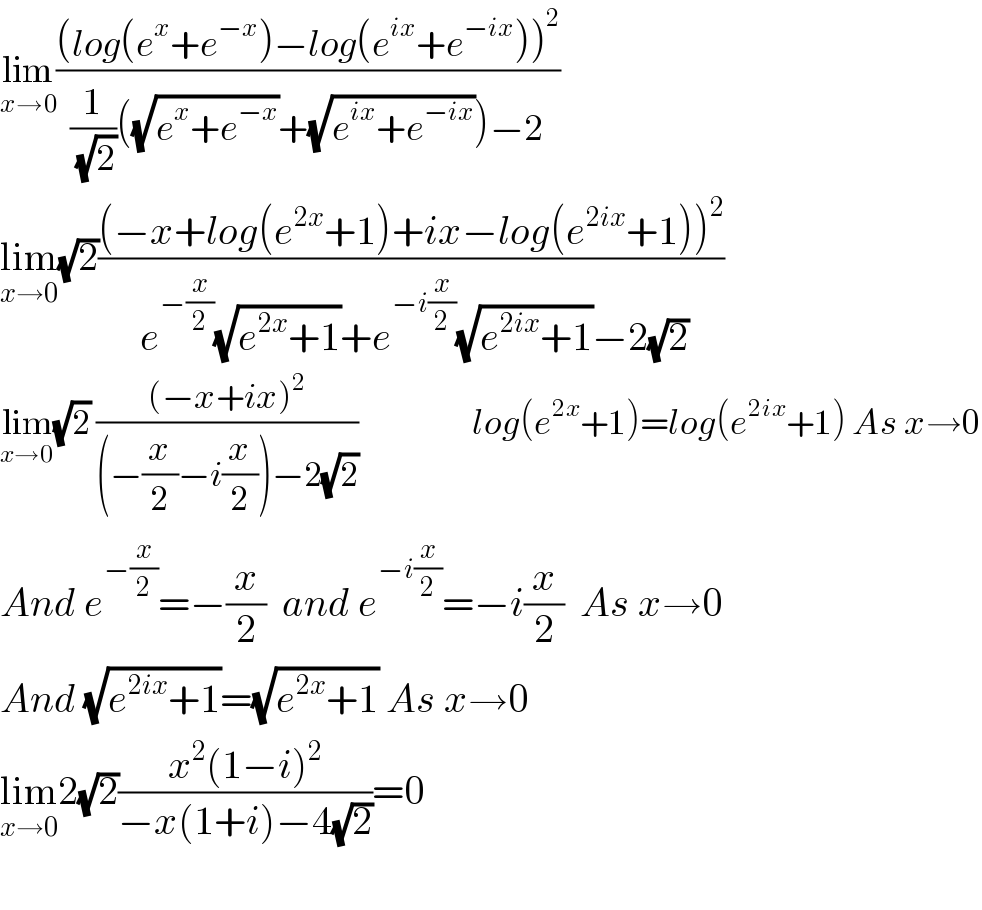
lim_(x→0) (((log(e^x +e^(−x) )−log(e^(ix) +e^(−ix) ))^2 )/((1/( (√2)))((√(e^x +e^(−x) ))+(√(e^(ix) +e^(−ix) )))−2)) lim_(x→0) (√2)(((−x+log(e^(2x) +1)+ix−log(e^(2ix) +1))^2 )/( e^(−(x/2)) (√(e^(2x) +1))+e^(−i(x/2)) (√(e^(2ix) +1))−2(√2))) lim_(x→0) (√2) (((−x+ix)^2 )/((−(x/2)−i(x/2))−2(√2))) log(e^(2x) +1)=log(e^(2ix) +1) As x→0 And e^(−(x/2)) =−(x/2) and e^(−i(x/2)) =−i(x/2) As x→0 And (√(e^(2ix) +1))=(√(e^(2x) +1)) As x→0 lim_(x→0) 2(√2)((x^2 (1−i)^2 )/(−x(1+i)−4(√2)))=0
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({log}\left({e}^{{x}} +{e}^{−{x}} \right)−{log}\left({e}^{{ix}} +{e}^{−{ix}} \right)\right)^{\mathrm{2}} }{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{{e}^{{x}} +{e}^{−{x}} }+\sqrt{{e}^{{ix}} +{e}^{−{ix}} }\right)−\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt{\mathrm{2}}\frac{\left(−{x}+{log}\left({e}^{\mathrm{2}{x}} +\mathrm{1}\right)+{ix}−{log}\left({e}^{\mathrm{2}{ix}} +\mathrm{1}\right)\right)^{\mathrm{2}} }{\:{e}^{−\frac{{x}}{\mathrm{2}}} \sqrt{{e}^{\mathrm{2}{x}} +\mathrm{1}}+{e}^{−{i}\frac{{x}}{\mathrm{2}}} \sqrt{{e}^{\mathrm{2}{ix}} +\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt{\mathrm{2}}\:\frac{\left(−{x}+{ix}\right)^{\mathrm{2}} }{\left(−\frac{{x}}{\mathrm{2}}−{i}\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}\sqrt{\mathrm{2}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{log}\left({e}^{\mathrm{2}{x}} +\mathrm{1}\right)={log}\left({e}^{\mathrm{2}{ix}} +\mathrm{1}\right)\:{As}\:{x}\rightarrow\mathrm{0} \\ $$$${And}\:{e}^{−\frac{{x}}{\mathrm{2}}} =−\frac{{x}}{\mathrm{2}}\:\:{and}\:{e}^{−{i}\frac{{x}}{\mathrm{2}}} =−{i}\frac{{x}}{\mathrm{2}}\:\:{As}\:{x}\rightarrow\mathrm{0} \\ $$$${And}\:\sqrt{{e}^{\mathrm{2}{ix}} +\mathrm{1}}=\sqrt{{e}^{\mathrm{2}{x}} +\mathrm{1}}\:{As}\:{x}\rightarrow\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}2}\sqrt{\mathrm{2}}\frac{{x}^{\mathrm{2}} \left(\mathrm{1}−{i}\right)^{\mathrm{2}} }{−{x}\left(\mathrm{1}+{i}\right)−\mathrm{4}\sqrt{\mathrm{2}}}=\mathrm{0} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *