Menu Close

lim-x-0-log-tan-2-x-tan-2-2x-

Tinku Tara 0 Comments
Pin




Question Number 34516 by rahul 19 last updated on 07/May/18
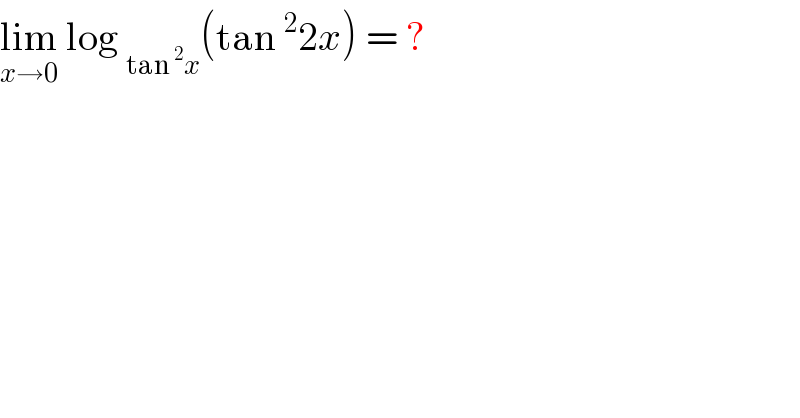
lim_(x→0) log _(tan^2 x) (tan^2 2x) = ?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{log}\:_{\mathrm{tan}\:^{\mathrm{2}} {x}} \left(\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}{x}\right)\:=\:? \\ $$
Commented by math khazana by abdo last updated on 08/May/18
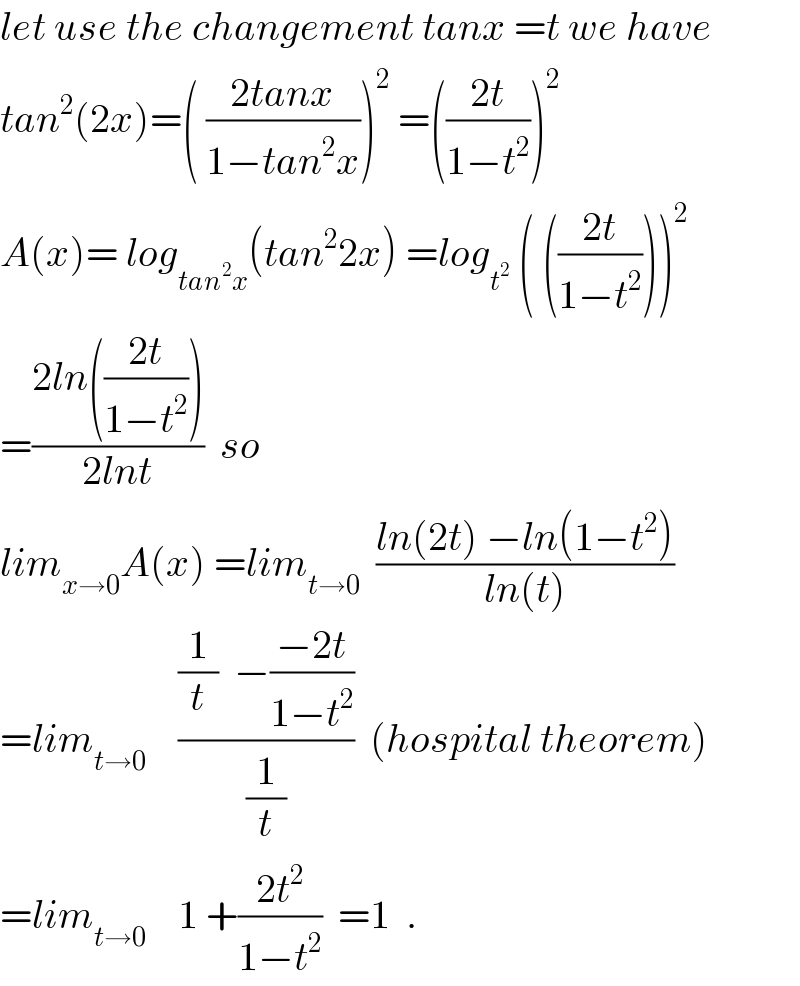
let use the changement tanx =t we have tan^2 (2x)=( ((2tanx)/(1−tan^2 x)))^2 =(((2t)/(1−t^2 )))^2 A(x)= log_(tan^2 x) (tan^2 2x) =log_t^2 ( (((2t)/(1−t^2 ))))^2 =((2ln(((2t)/(1−t^2 ))))/(2lnt)) so lim_(x→0) A(x) =lim_(t→0) ((ln(2t) −ln(1−t^2 ))/(ln(t))) =lim_(t→0) (((1/t) −((−2t)/(1−t^2 )))/(1/t)) (hospital theorem) =lim_(t→0) 1 +((2t^2 )/(1−t^2 )) =1 .
$${let}\:{use}\:{the}\:{changement}\:{tanx}\:={t}\:{we}\:{have} \\ $$$${tan}^{\mathrm{2}} \left(\mathrm{2}{x}\right)=\left(\:\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\right)^{\mathrm{2}} \:=\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$${A}\left({x}\right)=\:{log}_{{tan}^{\mathrm{2}} {x}} \left({tan}^{\mathrm{2}} \mathrm{2}{x}\right)\:={log}_{{t}^{\mathrm{2}} } \:\left(\:\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}{ln}\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)}{\mathrm{2}{lnt}}\:\:{so}\: \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {A}\left({x}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{2}{t}\right)\:−{ln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{{ln}\left({t}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\:\frac{\frac{\mathrm{1}}{{t}}\:\:−\frac{−\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }}{\frac{\mathrm{1}}{{t}}}\:\:\left({hospital}\:{theorem}\right) \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\:\mathrm{1}\:+\frac{\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }\:\:=\mathrm{1}\:\:. \\ $$
Answered by rahul 19 last updated on 07/May/18
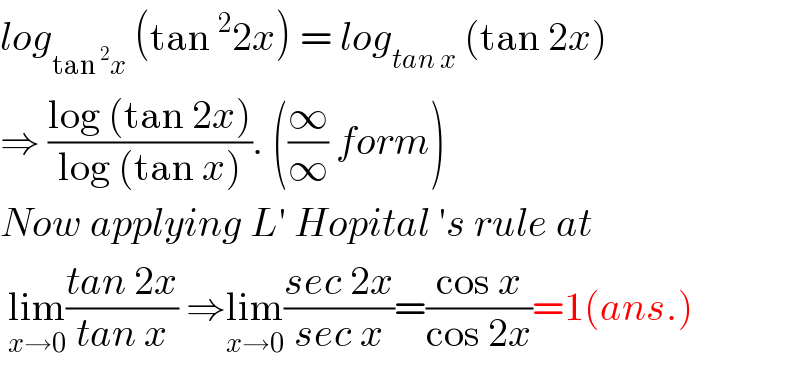
log_(tan^2 x) (tan^2 2x) = log_(tan x) (tan 2x) ⇒ ((log (tan 2x))/(log (tan x))). ((∞/∞) form) Now applying L′ Hopital ′s rule at lim_(x→0) ((tan 2x)/(tan x)) ⇒lim_(x→0) ((sec 2x)/(sec x))=((cos x)/(cos 2x))=1(ans.)
$${log}_{\mathrm{tan}\:^{\mathrm{2}} {x}} \:\left(\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}{x}\right)\:=\:{log}_{{tan}\:{x}} \:\left(\mathrm{tan}\:\mathrm{2}{x}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{log}\:\left(\mathrm{tan}\:\mathrm{2}{x}\right)}{\mathrm{log}\:\left(\mathrm{tan}\:{x}\right)}.\:\left(\frac{\infty}{\infty}\:{form}\right) \\ $$$${Now}\:{applying}\:{L}'\:{Hopital}\:'{s}\:{rule}\:{at}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{tan}\:\mathrm{2}{x}}{{tan}\:{x}}\:\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sec}\:\mathrm{2}{x}}{{sec}\:{x}}=\frac{\mathrm{cos}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}=\mathrm{1}\left({ans}.\right) \\ $$
Commented by MJS last updated on 07/May/18
it leads to the correct result in this case but you cannot just put away the logarithm because it′s not log ((tan 2x)/(tan x)) (here you could)
$$\mathrm{it}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{result}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{but} \\ $$$$\mathrm{you}\:\mathrm{cannot}\:\mathrm{just}\:\mathrm{put}\:\mathrm{away}\:\mathrm{the}\:\mathrm{logarithm}\:\mathrm{because} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{not} \\ $$$$\mathrm{log}\:\frac{\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{tan}\:{x}} \\ $$$$\left(\mathrm{here}\:\mathrm{you}\:\mathrm{could}\right) \\ $$
Commented by rahul 19 last updated on 07/May/18
So you mean final ans. match′ by chance′. Otherwise in this case method is wrong?
$${So}\:{you}\:{mean}\:{final}\:{ans}.\:{match}'\:{by}\:{chance}'. \\ $$$${Otherwise}\:{in}\:{this}\:{case}\:{method}\:{is}\:{wrong}? \\ $$
Commented by MJS last updated on 07/May/18
I think so, yes. You should be careful with this at a test...
$$\mathrm{I}\:\mathrm{think}\:\mathrm{so},\:\mathrm{yes}.\:\mathrm{You}\:\mathrm{should}\:\mathrm{be}\:\mathrm{careful}\:\mathrm{with} \\ $$$$\mathrm{this}\:\mathrm{at}\:\mathrm{a}\:\mathrm{test}… \\ $$
Answered by MJS last updated on 07/May/18
log_(tan^2 x) tan^2 2x=((ln tan^2 2x)/(ln tan^2 x))=((ln tan 2x)/(ln tan x)) (d/dx)(ln tan 2x)=2(1/(cos^2 2x))×(1/(tan 2x))= =(2/(cos 2x sin 2x))=(1/(cos x sin x cos 2x)) (d/dx)(ln tan x)=(1/(cos^2 x))×(1/(tan x))=(1/(cos x sin x)) ((1/(cos x sin x cos 2x))/(1/(cos x sin x)))=(1/(cos 2x)) lim_(x→0) (1/(cos 2x))=1
$$\mathrm{log}_{\mathrm{tan}^{\mathrm{2}} \:{x}} \mathrm{tan}^{\mathrm{2}} \:\mathrm{2}{x}=\frac{\mathrm{ln}\:\mathrm{tan}^{\mathrm{2}} \:\mathrm{2}{x}}{\mathrm{ln}\:\mathrm{tan}^{\mathrm{2}} \:{x}}=\frac{\mathrm{ln}\:\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{ln}\:\mathrm{tan}\:{x}} \\ $$$$\frac{{d}}{{dx}}\left(\mathrm{ln}\:\mathrm{tan}\:\mathrm{2}{x}\right)=\mathrm{2}\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}}×\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{2}{x}}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{cos}\:\mathrm{2}{x}\:\mathrm{sin}\:\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$\frac{{d}}{{dx}}\left(\mathrm{ln}\:\mathrm{tan}\:{x}\right)=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}×\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\frac{\mathrm{1}}{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:\mathrm{2}{x}}}{\frac{\mathrm{1}}{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}}}=\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{2}{x}}=\mathrm{1} \\ $$
Commented by rahul 19 last updated on 07/May/18
Thank you sir !

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *