Question Number 115167 by bemath last updated on 28/Sep/20
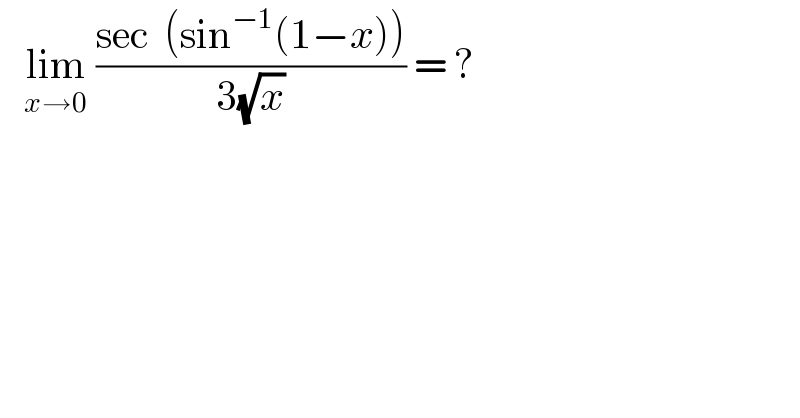
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\right)}{\mathrm{3}\sqrt{{x}}}\:=\:? \\ $$
Answered by bobhans last updated on 28/Sep/20
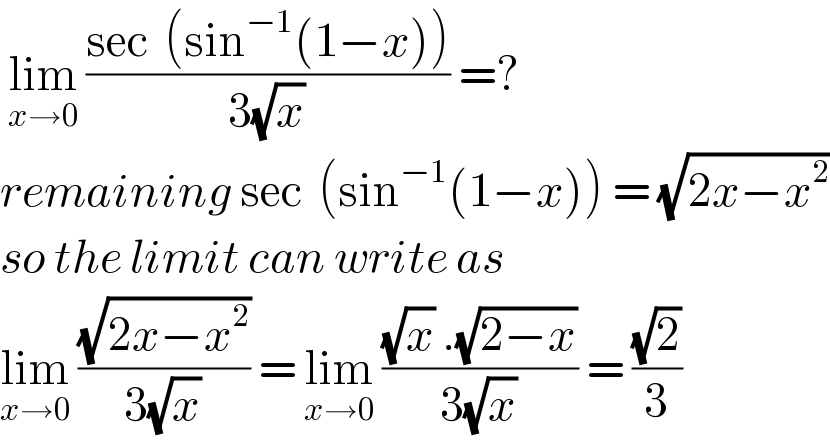
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\right)}{\mathrm{3}\sqrt{{x}}}\:=? \\ $$$${remaining}\:\mathrm{sec}\:\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\right)\:=\:\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} } \\ $$$${so}\:{the}\:{limit}\:{can}\:{write}\:{as}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}{\mathrm{3}\sqrt{{x}}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}}\:.\sqrt{\mathrm{2}−{x}}}{\mathrm{3}\sqrt{{x}}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
