Question Number 113747 by faysal last updated on 15/Sep/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{−\mathrm{1}} {x}}{{x}} \\ $$
Answered by bemath last updated on 15/Sep/20
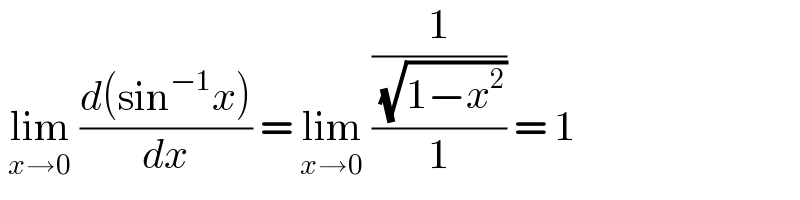
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{d}\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)}{{dx}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}{\mathrm{1}}\:=\:\mathrm{1} \\ $$
Answered by Olaf last updated on 15/Sep/20
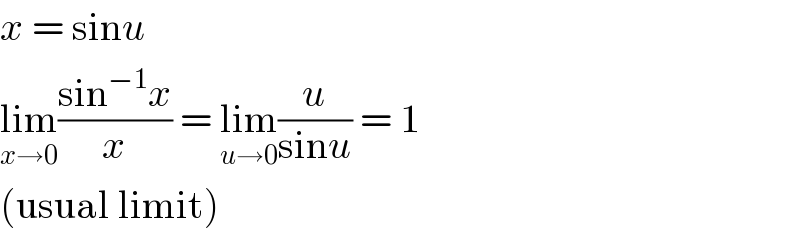
$${x}\:=\:\mathrm{sin}{u} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{−\mathrm{1}} {x}}{{x}}\:=\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}}{\mathrm{sin}{u}}\:=\:\mathrm{1} \\ $$$$\left(\mathrm{usual}\:\mathrm{limit}\right) \\ $$
Commented by Ar Brandon last updated on 15/Sep/20
Salut monsieur. Heureux de vous revoir��
Answered by Dwaipayan Shikari last updated on 15/Sep/20
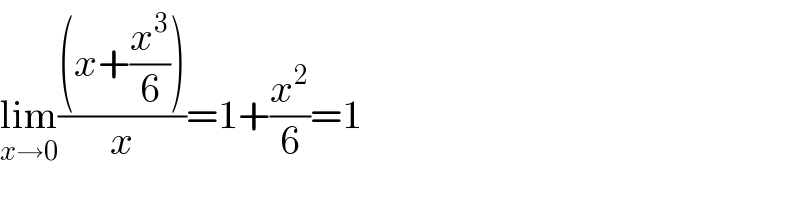
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{{x}}=\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}=\mathrm{1} \\ $$
