Question Number 106398 by bobhans last updated on 05/Aug/20
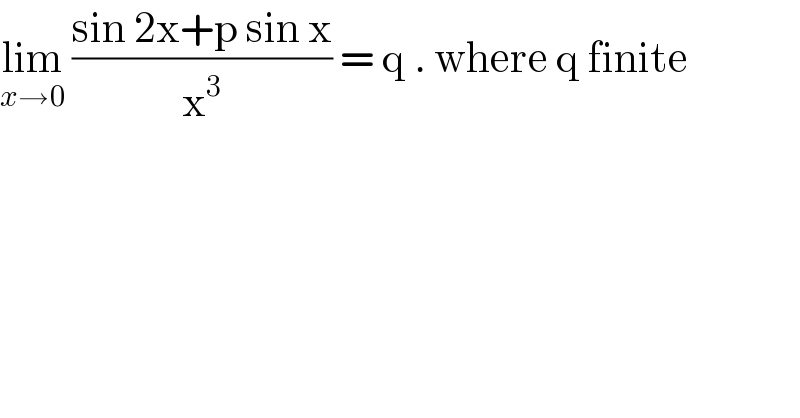
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2x}+\mathrm{p}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{q}\:.\:\mathrm{where}\:\mathrm{q}\:\mathrm{finite}\: \\ $$
Answered by bemath last updated on 05/Aug/20
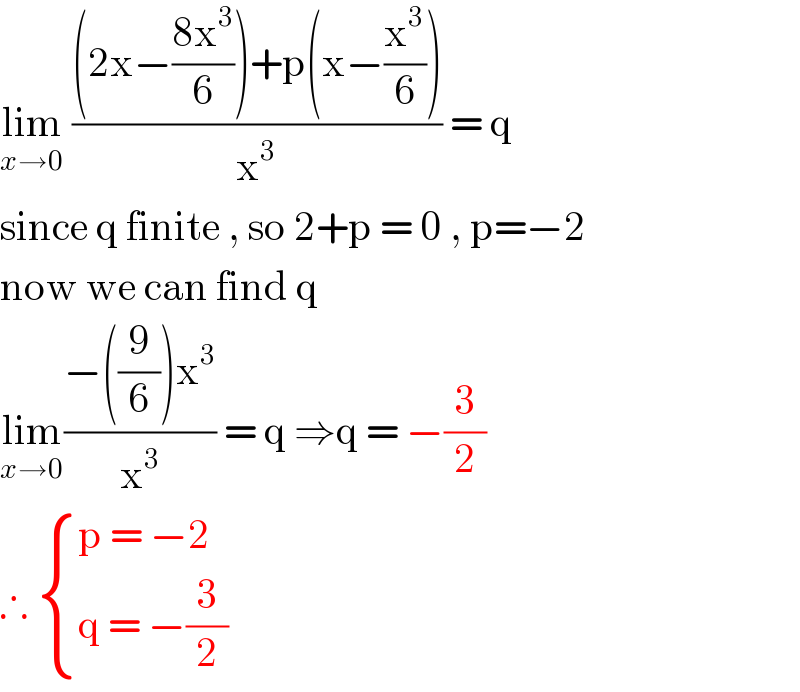
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{2x}−\frac{\mathrm{8x}^{\mathrm{3}} }{\mathrm{6}}\right)+\mathrm{p}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{q} \\ $$$$\mathrm{since}\:\mathrm{q}\:\mathrm{finite}\:,\:\mathrm{so}\:\mathrm{2}+\mathrm{p}\:=\:\mathrm{0}\:,\:\mathrm{p}=−\mathrm{2} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{q} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\left(\frac{\mathrm{9}}{\mathrm{6}}\right)\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{q}\:\Rightarrow\mathrm{q}\:=\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\therefore\:\begin{cases}{\mathrm{p}\:=\:−\mathrm{2}}\\{\mathrm{q}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$
Commented by bobhans last updated on 05/Aug/20

$$\mathrm{good} \\ $$
