Question Number 103255 by Study last updated on 13/Jul/20
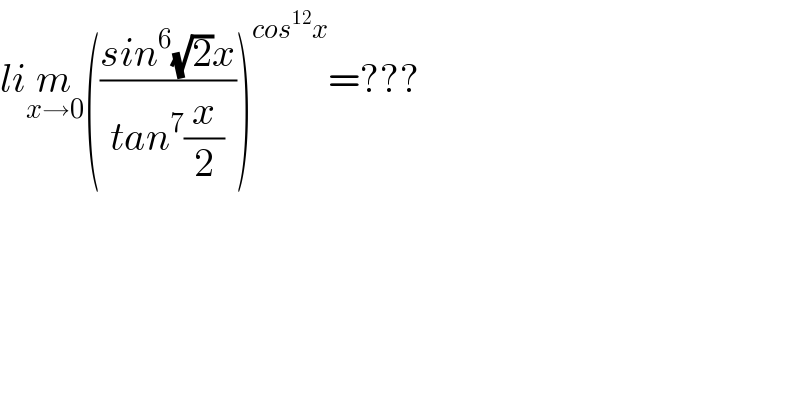
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left(\frac{{sin}^{\mathrm{6}} \sqrt{\mathrm{2}}{x}}{{tan}^{\mathrm{7}} \frac{{x}}{\mathrm{2}}}\right)^{{cos}^{\mathrm{12}} {x}} =??? \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20

$$\mathrm{May}\:\mathrm{be}\:\mathrm{infinity} \\ $$
Answered by OlafThorendsen last updated on 13/Jul/20

$$\mathrm{sin}{u}\:\underset{\mathrm{0}} {\sim}\:{u} \\ $$$$\mathrm{tan}{u}\:\underset{\mathrm{0}} {\sim}\:{u} \\ $$$$\mathrm{Then}\:\frac{\mathrm{sin}^{\mathrm{6}} \sqrt{\mathrm{2}}{x}}{\mathrm{tan}^{\mathrm{7}} \frac{{x}}{\mathrm{2}}}\:\underset{\mathrm{0}} {\sim}\:\frac{\left(\sqrt{\mathrm{2}}{x}\right)^{\mathrm{6}} }{\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{7}} }\:=\:\frac{\mathrm{2}^{\mathrm{3}} {x}^{\mathrm{6}} }{\frac{{x}^{\mathrm{7}} }{\mathrm{2}^{\mathrm{7}} }}\:=\:\frac{\mathrm{1024}}{{x}} \\ $$$$\mathrm{And}\:\mathrm{cos}{x}\:\underset{\mathrm{0}} {\sim}\:\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\:\mathrm{cos}^{\mathrm{12}} {x}\:\underset{\mathrm{0}} {\sim}\:\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}^{\mathrm{6}} \sqrt{\mathrm{2}}{x}}{\mathrm{tan}^{\mathrm{7}} \frac{{x}}{\mathrm{2}}}\right)^{\mathrm{cos}^{\mathrm{12}} {x}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1024}}{{x}}\right)^{\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}^{\mathrm{6}} \sqrt{\mathrm{2}}{x}}{\mathrm{tan}^{\mathrm{7}} \frac{{x}}{\mathrm{2}}}\right)^{\mathrm{cos}^{\mathrm{12}} {x}} =\:\begin{cases}{−\infty\:\mathrm{if}\:{x}<\mathrm{0}}\\{+\infty\:\mathrm{if}\:{x}>\mathrm{0}}\end{cases} \\ $$$$ \\ $$
Commented by Study last updated on 14/Jul/20
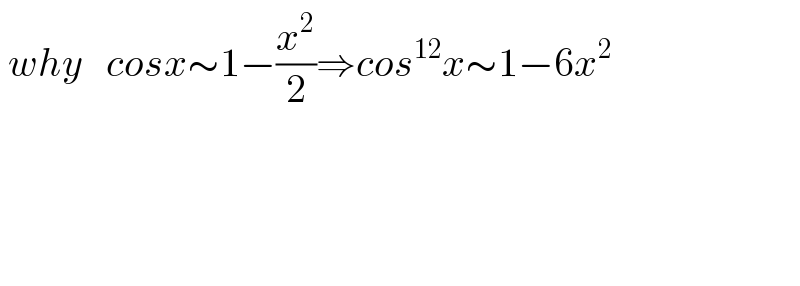
$$\:{why}\:\:\:{cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow{cos}^{\mathrm{12}} {x}\sim\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\: \\ $$
Commented by OlafThorendsen last updated on 14/Jul/20
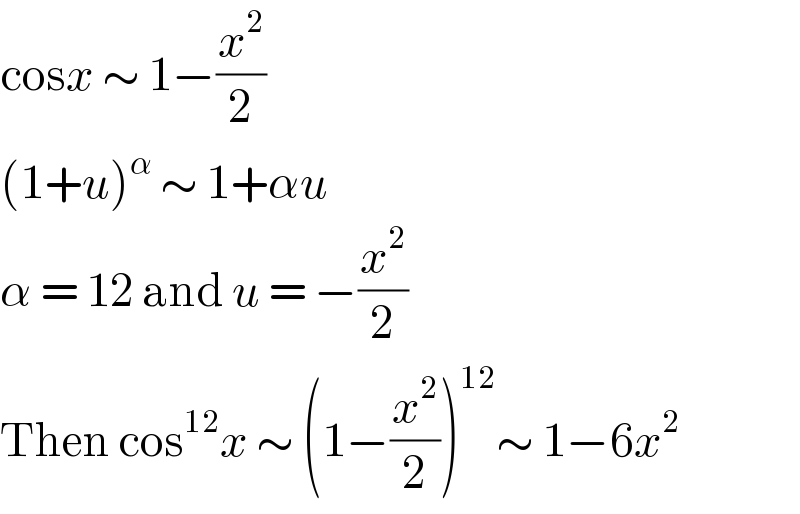
$$\mathrm{cos}{x}\:\sim\:\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{u}\right)^{\alpha} \:\sim\:\mathrm{1}+\alpha{u} \\ $$$$\alpha\:=\:\mathrm{12}\:\mathrm{and}\:{u}\:=\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{Then}\:\mathrm{cos}^{\mathrm{12}} {x}\:\sim\:\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{12}} \sim\:\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} \\ $$
