Question Number 101148 by john santu last updated on 30/Jun/20
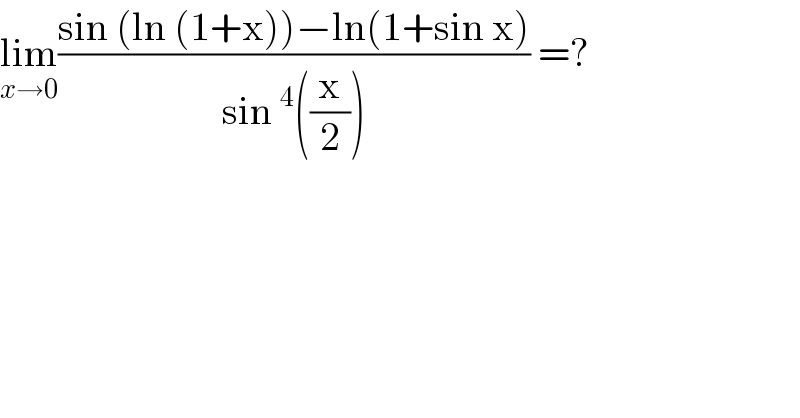
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{ln}\:\left(\mathrm{1}+\mathrm{x}\right)\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{sin}\:^{\mathrm{4}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}\:=?\: \\ $$
Commented by bramlex last updated on 01/Jul/20
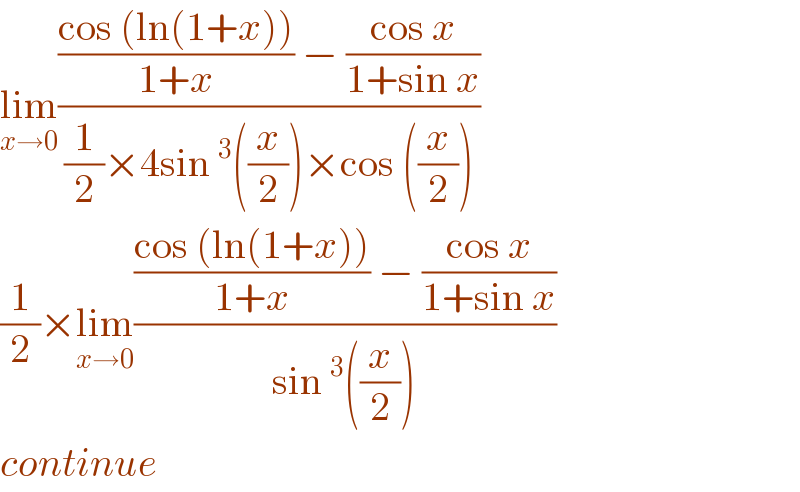
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{cos}\:\left(\mathrm{ln}\left(\mathrm{1}+{x}\right)\right)}{\mathrm{1}+{x}}\:−\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}}{\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4sin}\:^{\mathrm{3}} \left(\frac{{x}}{\mathrm{2}}\right)×\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{cos}\:\left(\mathrm{ln}\left(\mathrm{1}+{x}\right)\right)}{\mathrm{1}+{x}}\:−\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}}{\mathrm{sin}\:^{\mathrm{3}} \left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$${continue} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
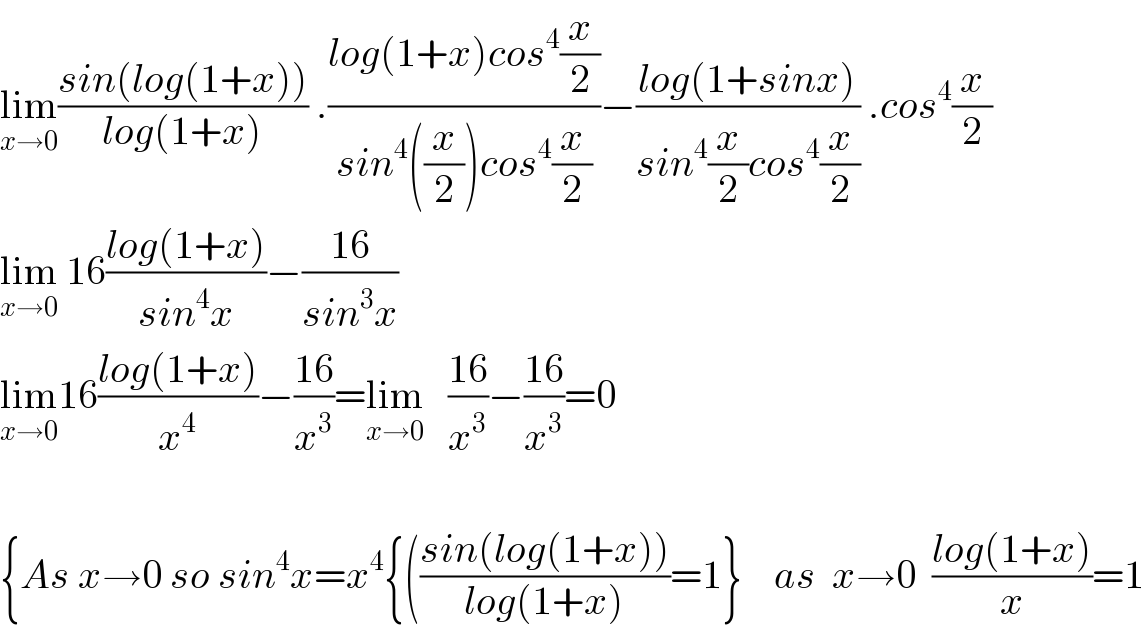
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left({log}\left(\mathrm{1}+{x}\right)\right)}{{log}\left(\mathrm{1}+{x}\right)}\:.\frac{{log}\left(\mathrm{1}+{x}\right){cos}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}}{{sin}^{\mathrm{4}} \left(\frac{{x}}{\mathrm{2}}\right){cos}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}}−\frac{{log}\left(\mathrm{1}+{sinx}\right)}{{sin}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}{cos}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}}\:.{cos}^{\mathrm{4}} \frac{{x}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{16}\frac{{log}\left(\mathrm{1}+{x}\right)}{{sin}^{\mathrm{4}} {x}}−\frac{\mathrm{16}}{{sin}^{\mathrm{3}} {x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}16}\frac{{log}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{4}} }−\frac{\mathrm{16}}{{x}^{\mathrm{3}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{16}}{{x}^{\mathrm{3}} }−\frac{\mathrm{16}}{{x}^{\mathrm{3}} }=\mathrm{0} \\ $$$$ \\ $$$$\left\{{As}\:{x}\rightarrow\mathrm{0}\:{so}\:{sin}^{\mathrm{4}} {x}={x}^{\mathrm{4}} \left\{\left(\frac{{sin}\left({log}\left(\mathrm{1}+{x}\right)\right)}{{log}\left(\mathrm{1}+{x}\right)}=\mathrm{1}\right\}\:\:\:\:{as}\:\:{x}\rightarrow\mathrm{0}\:\:\frac{{log}\left(\mathrm{1}+{x}\right)}{{x}}=\mathrm{1}\right.\right. \\ $$
