Menu Close

lim-x-0-sin-picos-2-x-3x-2-

Tinku Tara 0 Comments
Pin




Question Number 105106 by bemath last updated on 26/Jul/20
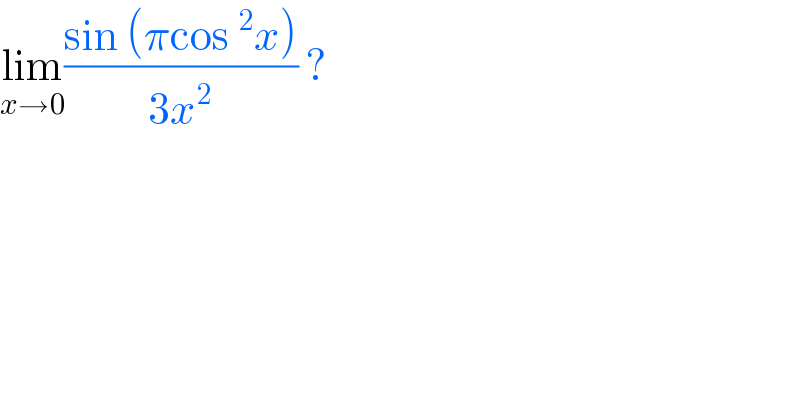
lim_(x→0) ((sin (πcos^2 x))/(3x^2 )) ?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\pi\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\:? \\ $$
Answered by bramlex last updated on 26/Jul/20
lim_(x→0) ((sin (π cos^2 x))/(3x^2 )) = lim_(x→0) ((−2πcos xsin x. cos (πcos^2 x))/(6x)) lim_(x→0) ((−πsin (2x).cos (πcos^2 x))/(6x)) = lim_(x→0) {−πcos (πcos^2 x)}.lim_(x→0) ((sin (2x))/(6x)) = (π/3) ▲
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\pi\:\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\pi\mathrm{cos}\:{x}\mathrm{sin}\:{x}.\:\mathrm{cos}\:\left(\pi\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{6}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\pi\mathrm{sin}\:\left(\mathrm{2}{x}\right).\mathrm{cos}\:\left(\pi\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{6}{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{−\pi\mathrm{cos}\:\left(\pi\mathrm{cos}\:^{\mathrm{2}} {x}\right)\right\}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{2}{x}\right)}{\mathrm{6}{x}} \\ $$$$=\:\frac{\pi}{\mathrm{3}}\:\blacktriangle \\ $$
Answered by OlafThorendsen last updated on 26/Jul/20
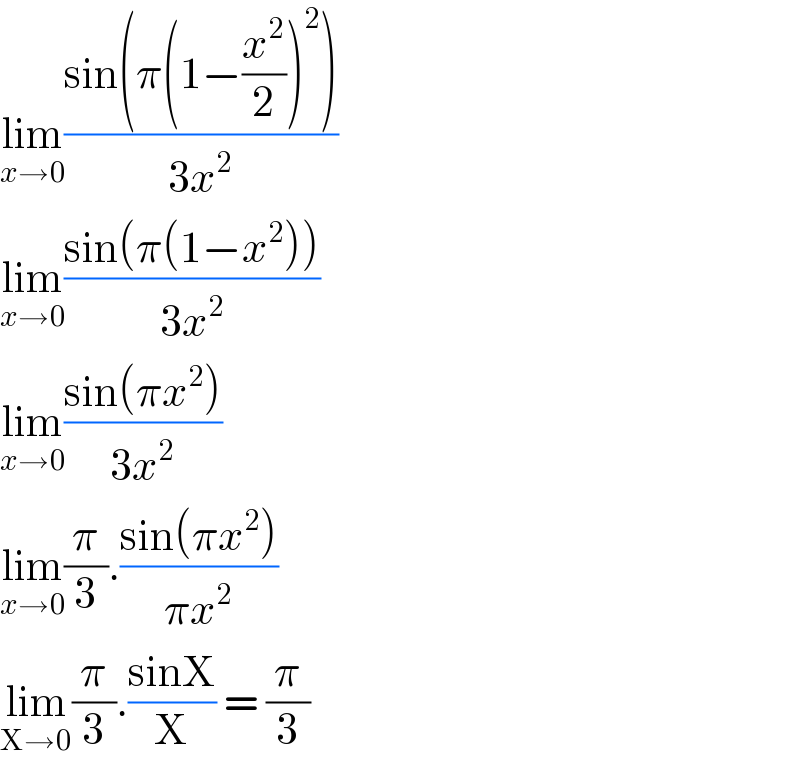
lim_(x→0) ((sin(π(1−(x^2 /2))^2 ))/(3x^2 )) lim_(x→0) ((sin(π(1−x^2 )))/(3x^2 )) lim_(x→0) ((sin(πx^2 ))/(3x^2 )) lim_(x→0) (π/3).((sin(πx^2 ))/(πx^2 )) lim_(X→0) (π/3).((sinX)/X) = (π/3)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\pi\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} \right)}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\pi\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right)}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\pi{x}^{\mathrm{2}} \right)}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\pi}{\mathrm{3}}.\frac{\mathrm{sin}\left(\pi{x}^{\mathrm{2}} \right)}{\pi{x}^{\mathrm{2}} } \\ $$$$\underset{\mathrm{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\pi}{\mathrm{3}}.\frac{\mathrm{sinX}}{\mathrm{X}}\:=\:\frac{\pi}{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 26/Jul/20
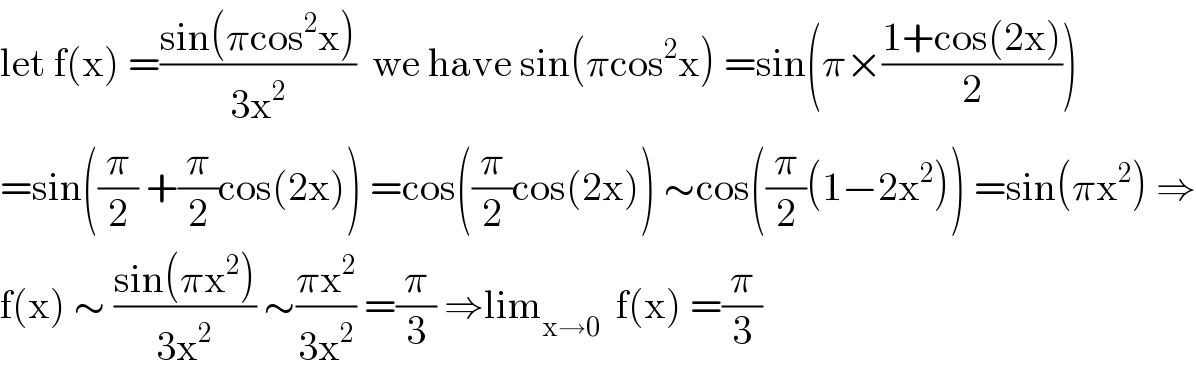
let f(x) =((sin(πcos^2 x))/(3x^2 )) we have sin(πcos^2 x) =sin(π×((1+cos(2x))/2)) =sin((π/2) +(π/2)cos(2x)) =cos((π/2)cos(2x)) ∼cos((π/2)(1−2x^2 )) =sin(πx^2 ) ⇒ f(x) ∼ ((sin(πx^2 ))/(3x^2 )) ∼((πx^2 )/(3x^2 )) =(π/3) ⇒lim_(x→0) f(x) =(π/3)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{sin}\left(\pi\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{3x}^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{sin}\left(\pi\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\:=\mathrm{sin}\left(\pi×\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right) \\ $$$$=\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2x}\right)\right)\:=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2x}\right)\right)\:\sim\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)\right)\:=\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\sim\:\frac{\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{3x}^{\mathrm{2}} }\:\sim\frac{\pi\mathrm{x}^{\mathrm{2}} }{\mathrm{3x}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\pi}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *