Menu Close

lim-x-0-sin-picos-2-x-x-2-why-it-can-not-be-solved-this-way-lim-x-0-sin-picos-2-x-x-2-lim-x-0-sin-picos-2-x-picos-2-x-lim-x-0-picos-2-x-x-2-pi-lim-x-0-cos-2-x-x-2

Tinku Tara 0 Comments
Pin




Question Number 60386 by Kunal12588 last updated on 20/May/19
lim_(x→0) ((sin(πcos^2 x))/x^2 ) why it can not be solved this way lim_(x→0) ((sin(πcos^2 x))/x^2 ) =lim_(x→0) ((sin(πcos^2 x))/(πcos^2 x))×lim_(x→0) ((πcos^2 x)/x^2 ) =π × lim_(x→0) ((cos^2 x)/x^2 ) but it is not equal to π
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$${why}\:{it}\:{can}\:{not}\:{be}\:{solved}\:{this}\:{way} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{\pi{cos}^{\mathrm{2}} {x}}×\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\pi{cos}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} } \\ $$$$=\pi\:×\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{cos}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} } \\ $$$${but}\:{it}\:{is}\:{not}\:{equal}\:{to}\:\pi \\ $$
Commented by mr W last updated on 20/May/19
lim_(x→0) ((sin(πcos^2 x))/(πcos^2 x))=((sin π)/(π×1))=(0/π)=0≠π lim_(x→0) ((πcos^2 x)/x^2 )=(π/0)→∞
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{\pi{cos}^{\mathrm{2}} {x}}=\frac{\mathrm{sin}\:\pi}{\pi×\mathrm{1}}=\frac{\mathrm{0}}{\pi}=\mathrm{0}\neq\pi \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\pi{cos}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }=\frac{\pi}{\mathrm{0}}\rightarrow\infty \\ $$
Commented by mr W last updated on 20/May/19
or lim_(x→0) ((sin(πcos^2 x))/x^2 ) (→(0/0)) =lim_(x→0) ((cos (πcos^2 x)(− π 2 cos x sin x))/(2x)) =lim_(x→0) (((−1)(− π) sin x)/x) =π lim_(x→0) ((sin x)/x) =π
$${or} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} }\:\:\:\:\left(\rightarrow\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{cos}\:\left(\pi{cos}^{\mathrm{2}} {x}\right)\left(−\:\pi\:\mathrm{2}\:\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}\right)}{\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\left(−\mathrm{1}\right)\left(−\:\pi\right)\:\mathrm{sin}\:{x}}{{x}} \\ $$$$=\pi\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{sin}\:{x}}{{x}} \\ $$$$=\pi \\ $$
Commented by prakash jain last updated on 20/May/19
Limit of product of two function = product of limits this is only true if both limit exist and finite.
Commented by Mr X pcx last updated on 20/May/19
another way we hsve cosx∼1−(x^2 /2) ⇒ cos^2 x ∼1−x^2 +(x^4 /4) ∼1−x^2 +o(x^4 ) ⇒ πcos^2 x∼π−π x^2 ⇒((sin(πcos^2 x))/x^2 ) ∼ ((sin(πx^2 ))/x^2 ) ∼((πx^2 )/x^2 ) (=π) ⇒ lim_(x−0) ((sin(π cos^2 x))/x^2 ) =π .
$${another}\:{way}\:\:{we}\:{hsve}\:{cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${cos}^{\mathrm{2}} {x}\:\sim\mathrm{1}−{x}^{\mathrm{2}} \:+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:\sim\mathrm{1}−{x}^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$$\pi{cos}^{\mathrm{2}} {x}\sim\pi−\pi\:{x}^{\mathrm{2}} \:\Rightarrow\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$\sim\:\frac{{sin}\left(\pi{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\:\sim\frac{\pi{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:\left(=\pi\right)\:\Rightarrow \\ $$$${lim}_{{x}−\mathrm{0}} \frac{{sin}\left(\pi\:{cos}^{\mathrm{2}} {x}\right)}{\overset{\mathrm{2}} {{x}}}\:=\pi\:. \\ $$
Answered by mr W last updated on 20/May/19
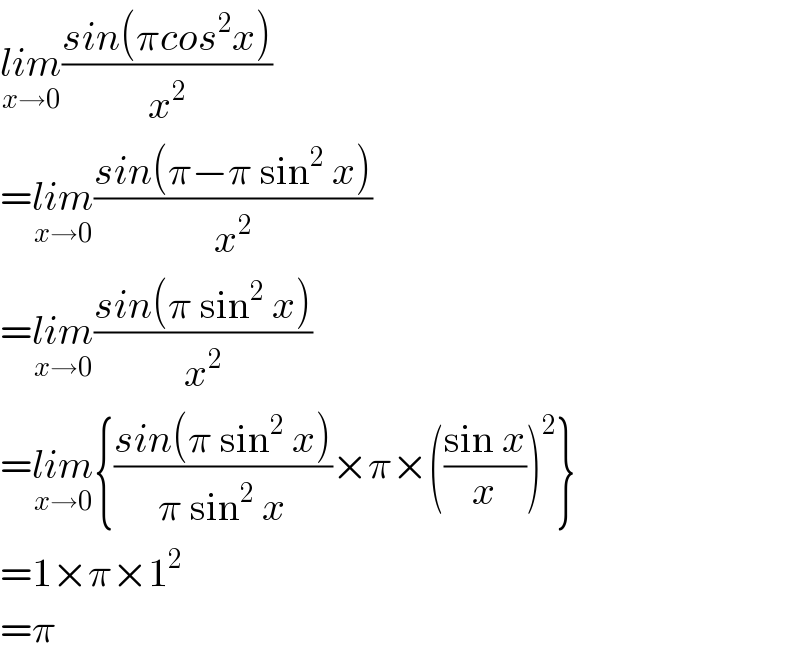
lim_(x→0) ((sin(πcos^2 x))/x^2 ) =lim_(x→0) ((sin(π−π sin^2 x))/x^2 ) =lim_(x→0) ((sin(π sin^2 x))/x^2 ) =lim_(x→0) {((sin(π sin^2 x))/(π sin^2 x))×π×(((sin x)/x))^2 } =1×π×1^2 =π
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\left(\pi{cos}^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\left(\pi−\pi\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\left(\pi\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left\{\frac{{sin}\left(\pi\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)}{\pi\:\mathrm{sin}^{\mathrm{2}} \:{x}}×\pi×\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} \right\} \\ $$$$=\mathrm{1}×\pi×\mathrm{1}^{\mathrm{2}} \\ $$$$=\pi \\ $$
Commented by Prithwish sen last updated on 20/May/19
Sir I think it will be lim_(x→0) ((sin(π−πcos^2 x))/x^2 ) (2^(nd) line) please check.
$$\mathrm{Sir}\:\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\: \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\mathrm{sin}\left(\pi−\pi\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\:\left(\mathrm{2}^{\mathrm{nd}} \:\mathrm{line}\right) \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by Kunal12588 last updated on 20/May/19
yes sir i know the answer this way but why it can not be solved the way i have written
$${yes}\:{sir}\:{i}\:{know}\:{the}\:{answer}\:{this}\:{way}\:{but} \\ $$$${why}\:{it}\:{can}\:{not}\:{be}\:{solved}\:{the}\:{way}\:{i}\:{have}\:{written} \\ $$
Commented by mr W last updated on 20/May/19
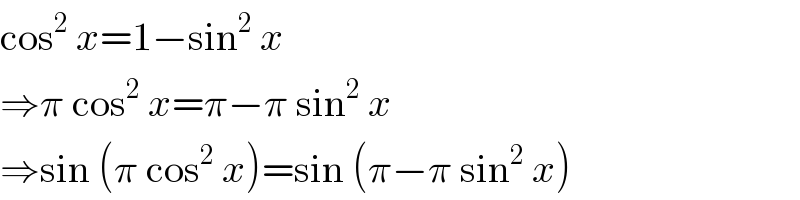
cos^2 x=1−sin^2 x ⇒π cos^2 x=π−π sin^2 x ⇒sin (π cos^2 x)=sin (π−π sin^2 x)
$$\mathrm{cos}^{\mathrm{2}} \:{x}=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\Rightarrow\pi\:\mathrm{cos}^{\mathrm{2}} \:{x}=\pi−\pi\:\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\pi\:\mathrm{cos}^{\mathrm{2}} \:{x}\right)=\mathrm{sin}\:\left(\pi−\pi\:\mathrm{sin}^{\mathrm{2}} \:{x}\right) \\ $$
Commented by Prithwish sen last updated on 21/May/19
Yes sir you are right. Please forgive .
$$\mathrm{Yes}\:\mathrm{sir}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}.\:\mathrm{Please}\:\mathrm{forgive}\:. \\ $$
Commented by mr W last updated on 22/May/19
no problem sir!
$${no}\:{problem}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *