Question Number 168166 by cortano1 last updated on 05/Apr/22
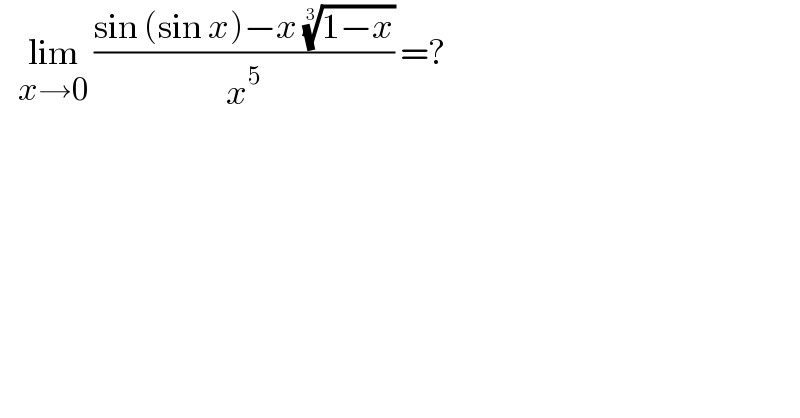
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)−{x}\:\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}}}{{x}^{\mathrm{5}} }\:=? \\ $$
Answered by qaz last updated on 05/Apr/22
![lim_(x→0) ((sin (sin x)−x((1−x))^(1/3) )/x^5 ) =lim_(x→0) ((sin (x−(1/6)x^3 +...)−x[1+ (((1/3)),(( 1)) )(−x)+ (((1/3)),(( 2)) )(−x)^2 + (((1/3)),(( 3)) )(−x)^3 + (((1/3)),(( 4)) )(−x)^4 +...])/x^5 ) =lim_(x→0) (([(x−(1/6)x^3 +(1/(120))x^5 +...)−(1/6)x^3 (1−(1/6)x^2 +...)^3 +(1/(120))x^5 (1−(1/6)x^2 +...)^5 +...]−x(1−(1/3)x−(1/9)x^2 −(5/(81))x^3 −((70)/(1944))x^4 +...))/x^5 ) =lim_(x→0) (((1/3)x^2 +o(x^2 ))/x^5 ) =±∞](https://www.tinkutara.com/question/Q168170.png)
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{sin}\:\mathrm{x}\right)−\mathrm{x}\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{x}}}{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} +…\right)−\mathrm{x}\left[\mathrm{1}+\begin{pmatrix}{\mathrm{1}/\mathrm{3}}\\{\:\:\:\mathrm{1}}\end{pmatrix}\left(−\mathrm{x}\right)+\begin{pmatrix}{\mathrm{1}/\mathrm{3}}\\{\:\:\:\mathrm{2}}\end{pmatrix}\left(−\mathrm{x}\right)^{\mathrm{2}} +\begin{pmatrix}{\mathrm{1}/\mathrm{3}}\\{\:\:\:\mathrm{3}}\end{pmatrix}\left(−\mathrm{x}\right)^{\mathrm{3}} +\begin{pmatrix}{\mathrm{1}/\mathrm{3}}\\{\:\:\:\mathrm{4}}\end{pmatrix}\left(−\mathrm{x}\right)^{\mathrm{4}} +…\right]}{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{120}}\mathrm{x}^{\mathrm{5}} +…\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} +…\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{120}}\mathrm{x}^{\mathrm{5}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} +…\right)^{\mathrm{5}} +…\right]−\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{81}}\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{70}}{\mathrm{1944}}\mathrm{x}^{\mathrm{4}} +…\right)}{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\pm\infty \\ $$
