Question Number 99676 by bemath last updated on 22/Jun/20
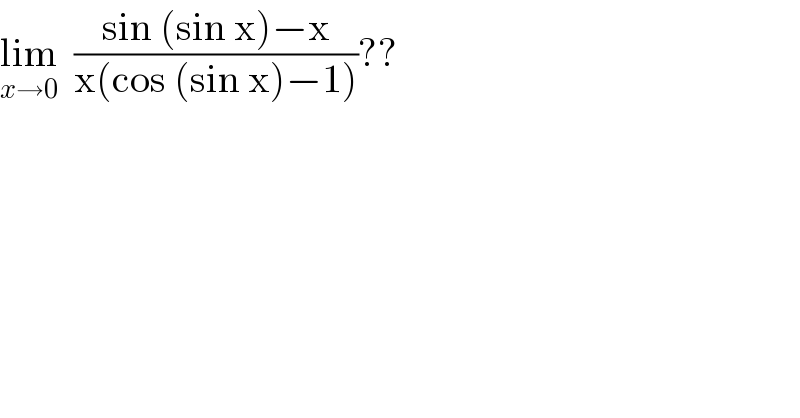
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{sin}\:\left(\mathrm{sin}\:\mathrm{x}\right)−\mathrm{x}}{\mathrm{x}\left(\mathrm{cos}\:\left(\mathrm{sin}\:\mathrm{x}\right)−\mathrm{1}\right)}?? \\ $$
Answered by bobhans last updated on 23/Jun/20
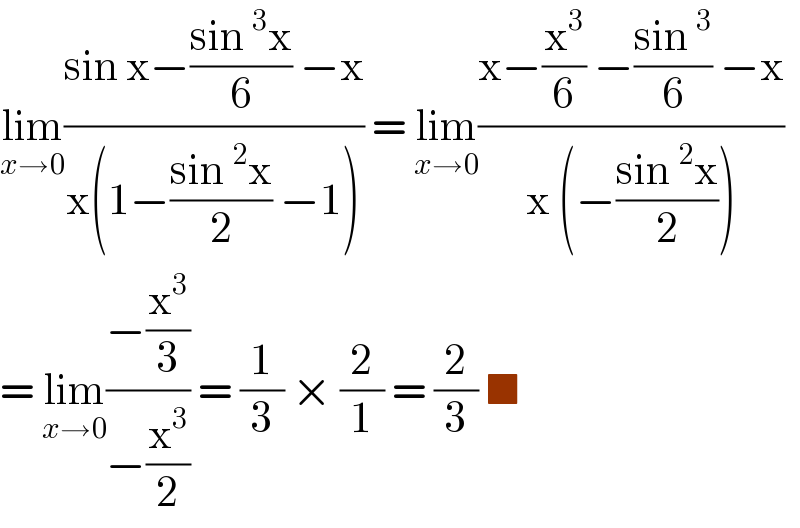
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}−\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{6}}\:−\mathrm{x}}{\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}\:−\mathrm{1}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:−\frac{\mathrm{sin}\:^{\mathrm{3}} }{\mathrm{6}}\:−\mathrm{x}}{\mathrm{x}\:\left(−\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}\right)} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}}{−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:×\:\frac{\mathrm{2}}{\mathrm{1}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\blacksquare \\ $$
