Question Number 169966 by cortano1 last updated on 13/May/22
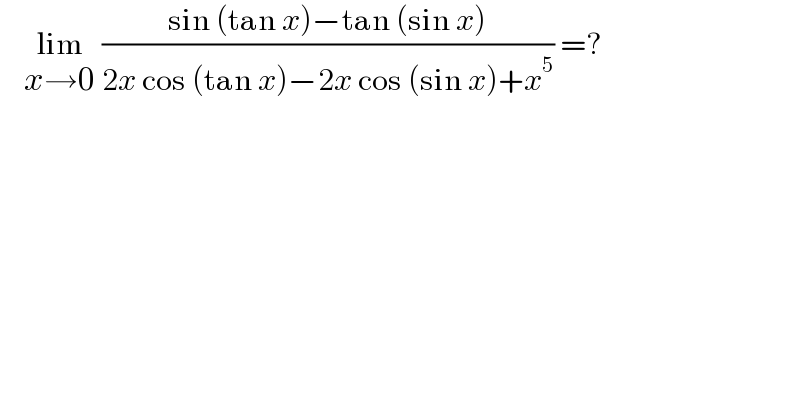
$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{tan}\:{x}\right)−\mathrm{tan}\:\left(\mathrm{sin}\:{x}\right)}{\mathrm{2}{x}\:\mathrm{cos}\:\left(\mathrm{tan}\:{x}\right)−\mathrm{2}{x}\:\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)+{x}^{\mathrm{5}} }\:=? \\ $$
Answered by qaz last updated on 13/May/22

$$\mathrm{sin}\:\mathrm{tan}\:\mathrm{x}=\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{40}}−\frac{\mathrm{55x}^{\mathrm{7}} }{\mathrm{1008}}+… \\ $$$$\mathrm{tan}\:\mathrm{sin}\:\mathrm{x}=\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{40}}−\frac{\mathrm{107x}^{\mathrm{7}} }{\mathrm{5040}}+… \\ $$$$\mathrm{2xcos}\:\mathrm{tan}\:\mathrm{x}=\mathrm{2x}−\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{7x}^{\mathrm{5}} }{\mathrm{12}}−\frac{\mathrm{97x}^{\mathrm{7}} }{\mathrm{360}}+… \\ $$$$\mathrm{2xcos}\:\mathrm{sin}\:\mathrm{x}=\mathrm{2x}−\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{5x}^{\mathrm{5}} }{\mathrm{12}}−\frac{\mathrm{37x}^{\mathrm{7}} }{\mathrm{360}}+… \\ $$$$… \\ $$
