Question Number 124010 by john_santu last updated on 30/Nov/20

$$\:\underset{{x}\rightarrow\mathrm{0}^{+} \:} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}+\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{3}{x}}}{\mathrm{tan}\:\left({x}\sqrt{\mathrm{2}}\right)}\right)= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}+\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{3}{x}}}{\mathrm{tan}\:\left({x}\sqrt{\mathrm{2}}\right)}\right)= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:{x}+\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{3}{x}}}{\mathrm{tan}\:\left({x}\sqrt{\mathrm{2}}\right)}\right)= \\ $$
Answered by liberty last updated on 30/Nov/20

$$\:\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{3}{x}}\:=\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\right.}\:=\:\sqrt{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)} \\ $$$$\:=\:\sqrt{\mathrm{2}}\:\mid\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mid\:=\:\rightarrow\begin{cases}{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:;\:{x}\geqslant\mathrm{0}}\\{−\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\:;\:{x}<\mathrm{0}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}+\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}{\mathrm{tan}\:\left({x}\sqrt{\mathrm{2}}\right)}\right)=\:\frac{\mathrm{1}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:=\:\frac{\sqrt{\mathrm{2}}+\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}−\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}{\mathrm{tan}\:\left({x}\sqrt{\mathrm{2}}\right)}\right)=\frac{\sqrt{\mathrm{2}}−\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}+\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{3}{x}}}{\mathrm{tan}\:\left({x}\sqrt{\mathrm{2}}\right)}\right)\:{doesn}'{t}\:{exist} \\ $$
Commented by Mammadli last updated on 30/Nov/20

Commented by john_santu last updated on 30/Nov/20
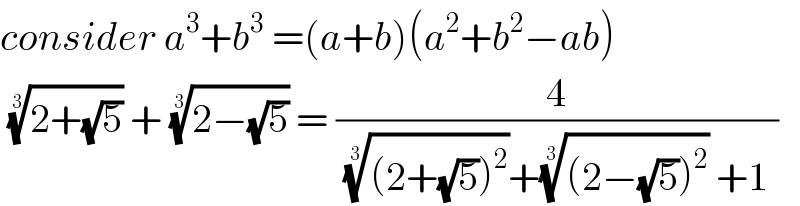
$${consider}\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} \:=\left({a}+{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right) \\ $$$$\:\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{4}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }\:+\mathrm{1}\:} \\ $$
Commented by malwan last updated on 30/Nov/20

$$=\:\mathrm{1} \\ $$
Commented by bharathkumar last updated on 30/Nov/20

$${sex} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Nov/20

$$\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}+\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\:={p} \\ $$$$\mathrm{2}+\sqrt{\mathrm{5}}+\mathrm{2}−\sqrt{\mathrm{5}}\:+\mathrm{3}\sqrt{\mathrm{4}−\mathrm{5}}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}+\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\right)={p}^{\mathrm{3}} \\ $$$$\mathrm{4}−\mathrm{3}{p}={p}^{\mathrm{3}} \\ $$$${p}=\mathrm{1} \\ $$
