Question Number 99968 by bobhans last updated on 24/Jun/20
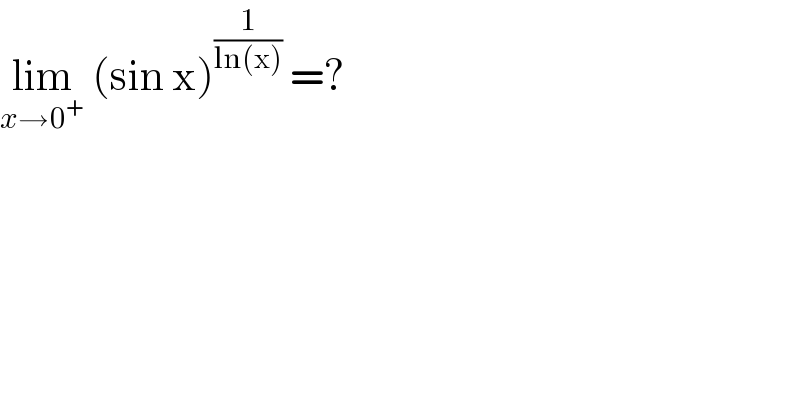
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\mathrm{sin}\:\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{ln}\left(\mathrm{x}\right)}} \:=?\: \\ $$
Commented by bobhans last updated on 24/Jun/20
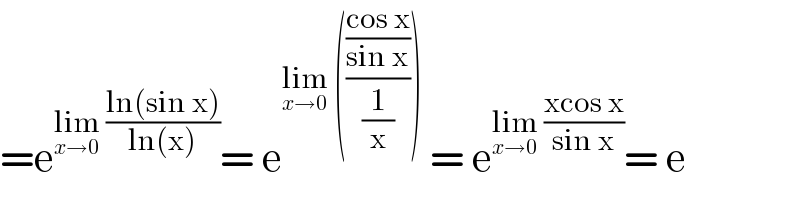
$$=\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{ln}\left(\mathrm{x}\right)}} =\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}}{\frac{\mathrm{1}}{\mathrm{x}}}\right)} \:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{xcos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}} =\:\mathrm{e} \\ $$
