Question Number 91020 by jagoll last updated on 27/Apr/20
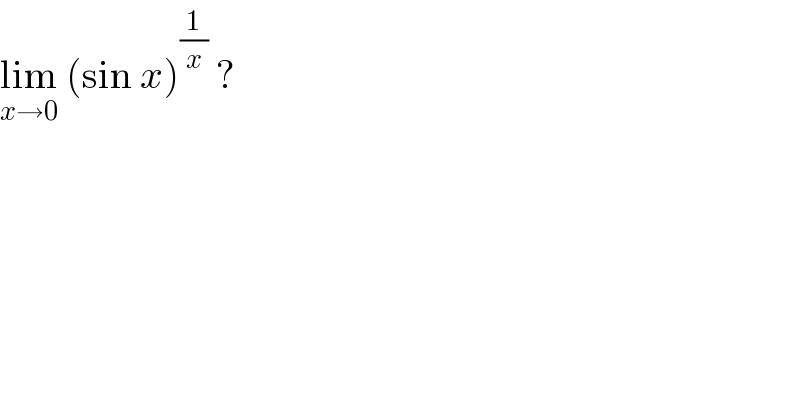
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{sin}\:{x}\right)^{\frac{\mathrm{1}}{{x}}} \:?\: \\ $$
Commented by jagoll last updated on 28/Apr/20
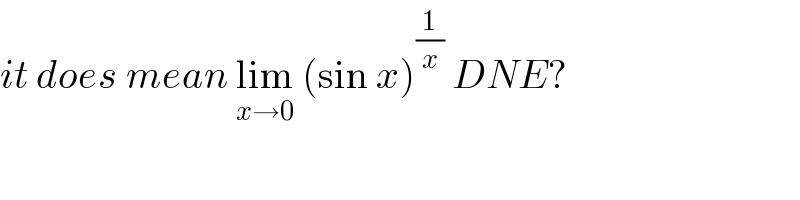
$${it}\:{does}\:{mean}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{sin}\:{x}\right)^{\frac{\mathrm{1}}{{x}}} \:{DNE}? \\ $$
Commented by mathmax by abdo last updated on 27/Apr/20
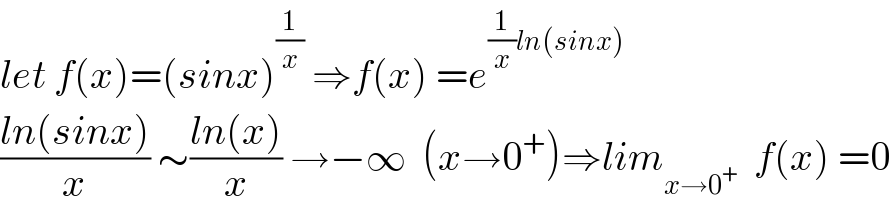
$${let}\:{f}\left({x}\right)=\left({sinx}\right)^{\frac{\mathrm{1}}{{x}}} \:\Rightarrow{f}\left({x}\right)\:={e}^{\frac{\mathrm{1}}{{x}}{ln}\left({sinx}\right)} \\ $$$$\frac{{ln}\left({sinx}\right)}{{x}}\:\sim\frac{{ln}\left({x}\right)}{{x}}\:\rightarrow−\infty\:\:\left({x}\rightarrow\mathrm{0}^{+} \right)\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:{f}\left({x}\right)\:=\mathrm{0} \\ $$
