Question Number 104350 by bemath last updated on 21/Jul/20
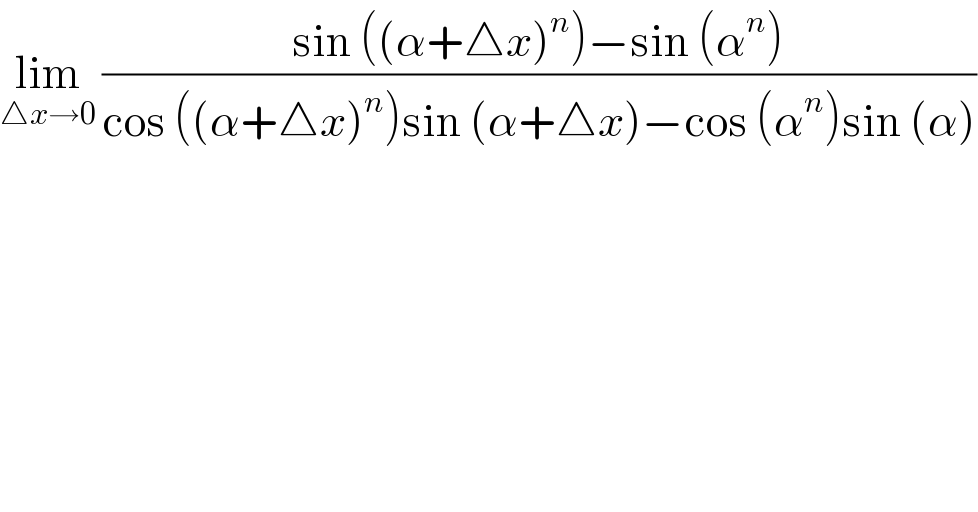
$$\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\left(\alpha+\bigtriangleup{x}\right)^{{n}} \right)−\mathrm{sin}\:\left(\alpha^{{n}} \right)}{\mathrm{cos}\:\left(\left(\alpha+\bigtriangleup{x}\right)^{{n}} \right)\mathrm{sin}\:\left(\alpha+\bigtriangleup{x}\right)−\mathrm{cos}\:\left(\alpha^{{n}} \right)\mathrm{sin}\:\left(\alpha\right)} \\ $$
Answered by john santu last updated on 21/Jul/20
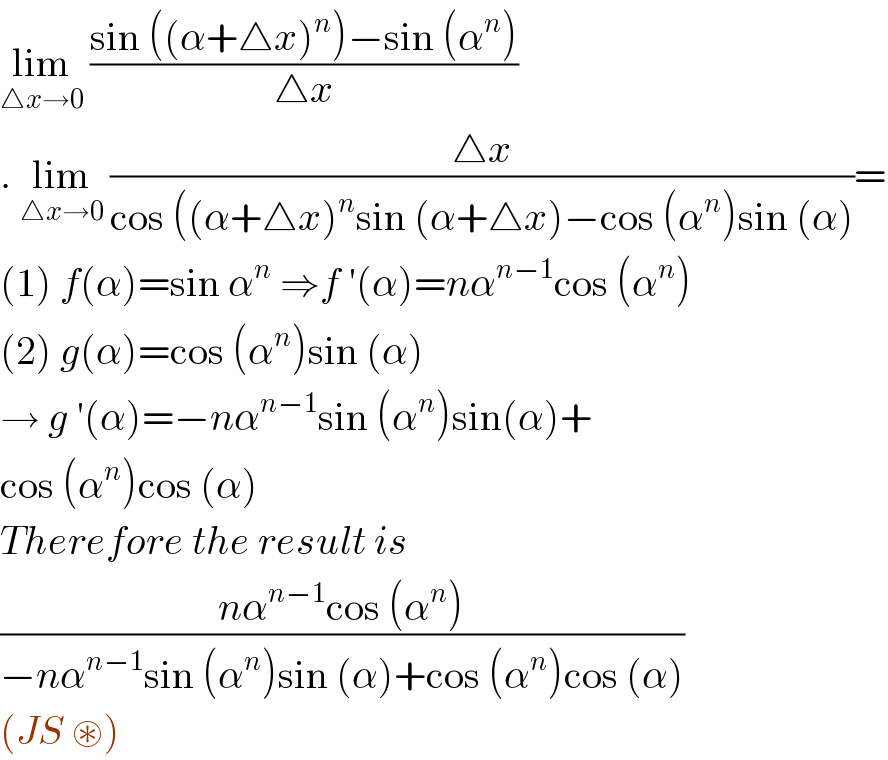
$$\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\left(\alpha+\bigtriangleup{x}\right)^{{n}} \right)−\mathrm{sin}\:\left(\alpha^{{n}} \right)}{\bigtriangleup{x}} \\ $$$$.\:\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\bigtriangleup{x}}{\mathrm{cos}\:\left(\left(\alpha+\bigtriangleup{x}\right)^{{n}} \mathrm{sin}\:\left(\alpha+\bigtriangleup{x}\right)−\mathrm{cos}\:\left(\alpha^{{n}} \right)\mathrm{sin}\:\left(\alpha\right)\right.}= \\ $$$$\left(\mathrm{1}\right)\:{f}\left(\alpha\right)=\mathrm{sin}\:\alpha^{{n}} \:\Rightarrow{f}\:'\left(\alpha\right)={n}\alpha^{{n}−\mathrm{1}} \mathrm{cos}\:\left(\alpha^{{n}} \right) \\ $$$$\left(\mathrm{2}\right)\:{g}\left(\alpha\right)=\mathrm{cos}\:\left(\alpha^{{n}} \right)\mathrm{sin}\:\left(\alpha\right) \\ $$$$\rightarrow\:{g}\:'\left(\alpha\right)=−{n}\alpha^{{n}−\mathrm{1}} \mathrm{sin}\:\left(\alpha^{{n}} \right)\mathrm{sin}\left(\alpha\right)+ \\ $$$$\mathrm{cos}\:\left(\alpha^{{n}} \right)\mathrm{cos}\:\left(\alpha\right) \\ $$$${Therefore}\:{the}\:{result}\:{is}\: \\ $$$$\frac{{n}\alpha^{{n}−\mathrm{1}} \mathrm{cos}\:\left(\alpha^{{n}} \right)}{−{n}\alpha^{{n}−\mathrm{1}} \mathrm{sin}\:\left(\alpha^{{n}} \right)\mathrm{sin}\:\left(\alpha\right)+\mathrm{cos}\:\left(\alpha^{{n}} \right)\mathrm{cos}\:\left(\alpha\right)} \\ $$$$\left({JS}\:\circledast\right) \\ $$
