Menu Close

lim-x-0-sin-x-sin-sin-x-x-3-

Tinku Tara 0 Comments
Pin




Question Number 34458 by rahul 19 last updated on 06/May/18
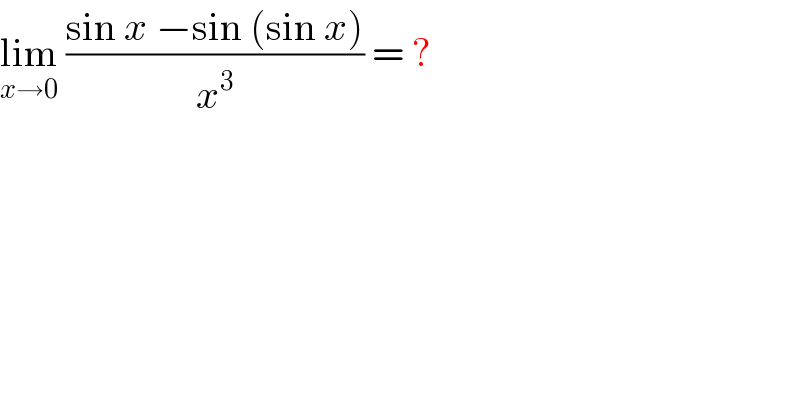
lim_(x→0) ((sin x −sin (sin x))/x^3 ) = ?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}\:−\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)}{{x}^{\mathrm{3}} }\:=\:? \\ $$
Commented by math khazana by abdo last updated on 06/May/18
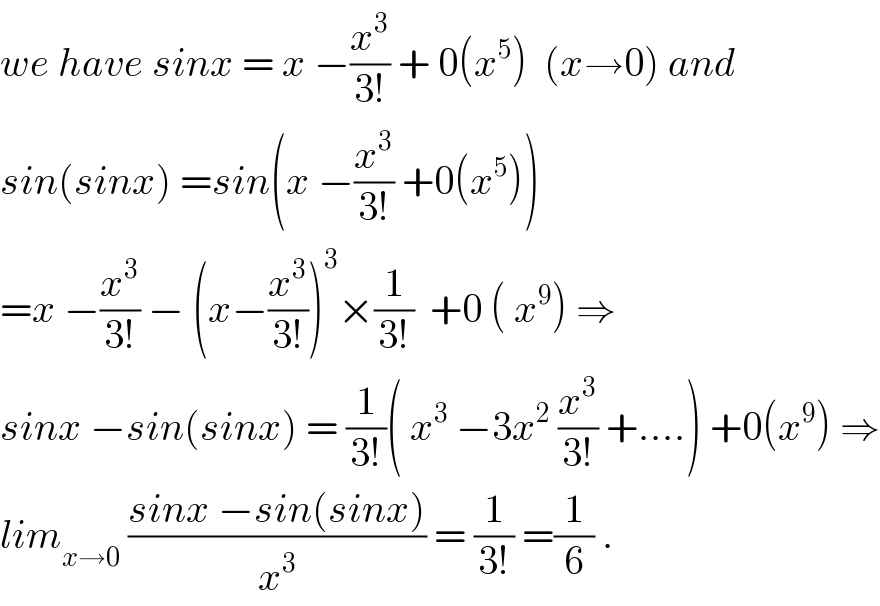
we have sinx = x −(x^3 /(3!)) + 0(x^5 ) (x→0) and sin(sinx) =sin(x −(x^3 /(3!)) +0(x^5 )) =x −(x^3 /(3!)) − (x−(x^3 /(3!)))^3 ×(1/(3!)) +0 ( x^9 ) ⇒ sinx −sin(sinx) = (1/(3!))( x^3 −3x^2 (x^3 /(3!)) +....) +0(x^9 ) ⇒ lim_(x→0) ((sinx −sin(sinx))/x^3 ) = (1/(3!)) =(1/6) .
$${we}\:{have}\:{sinx}\:=\:{x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\:\mathrm{0}\left({x}^{\mathrm{5}} \right)\:\:\left({x}\rightarrow\mathrm{0}\right)\:{and} \\ $$$${sin}\left({sinx}\right)\:={sin}\left({x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\mathrm{0}\left({x}^{\mathrm{5}} \right)\right) \\ $$$$={x}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:−\:\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)^{\mathrm{3}} ×\frac{\mathrm{1}}{\mathrm{3}!}\:\:+\mathrm{0}\:\left(\:{x}^{\mathrm{9}} \right)\:\Rightarrow \\ $$$${sinx}\:−{sin}\left({sinx}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}!}\left(\:{x}^{\mathrm{3}} \:−\mathrm{3}{x}^{\mathrm{2}} \:\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+….\right)\:+\mathrm{0}\left({x}^{\mathrm{9}} \right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{sinx}\:−{sin}\left({sinx}\right)}{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}!}\:=\frac{\mathrm{1}}{\mathrm{6}}\:. \\ $$
Commented by math khazana by abdo last updated on 06/May/18
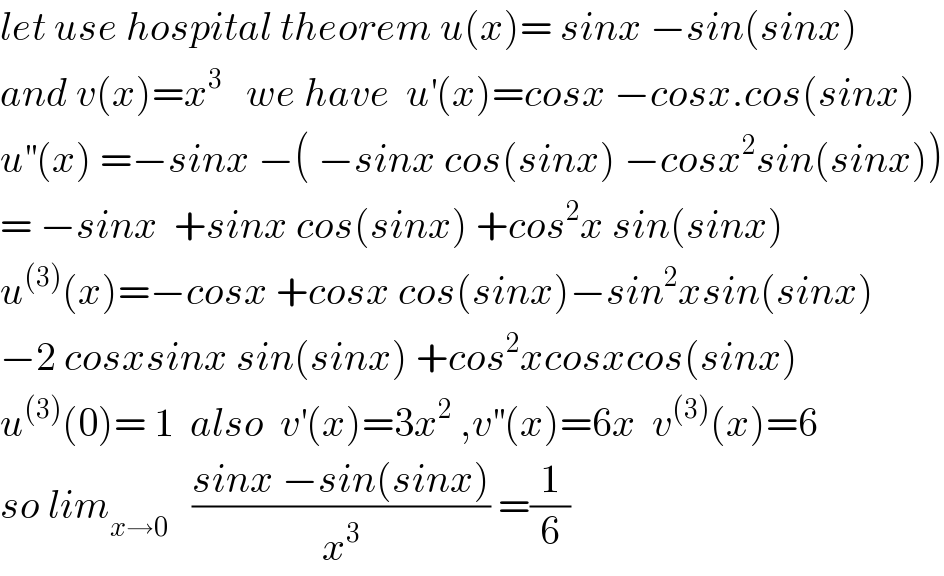
let use hospital theorem u(x)= sinx −sin(sinx) and v(x)=x^3 we have u^′ (x)=cosx −cosx.cos(sinx) u^(′′) (x) =−sinx −( −sinx cos(sinx) −cosx^2 sin(sinx)) = −sinx +sinx cos(sinx) +cos^2 x sin(sinx) u^((3)) (x)=−cosx +cosx cos(sinx)−sin^2 xsin(sinx) −2 cosxsinx sin(sinx) +cos^2 xcosxcos(sinx) u^((3)) (0)= 1 also v^′ (x)=3x^2 ,v^(′′) (x)=6x v^((3)) (x)=6 so lim_(x→0) ((sinx −sin(sinx))/x^3 ) =(1/6)
$${let}\:{use}\:{hospital}\:{theorem}\:{u}\left({x}\right)=\:{sinx}\:−{sin}\left({sinx}\right) \\ $$$${and}\:{v}\left({x}\right)={x}^{\mathrm{3}} \:\:\:{we}\:{have}\:\:{u}^{'} \left({x}\right)={cosx}\:−{cosx}.{cos}\left({sinx}\right) \\ $$$${u}^{''} \left({x}\right)\:=−{sinx}\:−\left(\:−{sinx}\:{cos}\left({sinx}\right)\:−{cosx}^{\mathrm{2}} {sin}\left({sinx}\right)\right) \\ $$$$=\:−{sinx}\:\:+{sinx}\:{cos}\left({sinx}\right)\:+{cos}^{\mathrm{2}} {x}\:{sin}\left({sinx}\right) \\ $$$${u}^{\left(\mathrm{3}\right)} \left({x}\right)=−{cosx}\:+{cosx}\:{cos}\left({sinx}\right)−{sin}^{\mathrm{2}} {xsin}\left({sinx}\right) \\ $$$$−\mathrm{2}\:{cosxsinx}\:{sin}\left({sinx}\right)\:+{cos}^{\mathrm{2}} {xcosxcos}\left({sinx}\right) \\ $$$${u}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\:\mathrm{1}\:\:{also}\:\:{v}^{'} \left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} \:,{v}^{''} \left({x}\right)=\mathrm{6}{x}\:\:{v}^{\left(\mathrm{3}\right)} \left({x}\right)=\mathrm{6} \\ $$$${so}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{sinx}\:−{sin}\left({sinx}\right)}{{x}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by math khazana by abdo last updated on 06/May/18
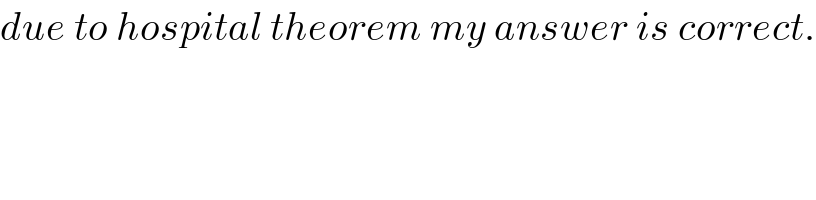
due to hospital theorem my answer is correct.
$${due}\:{to}\:{hospital}\:{theorem}\:{my}\:{answer}\:{is}\:{correct}. \\ $$
Commented by rahul 19 last updated on 07/May/18
Thank you sir !
Answered by tanmay.chaudhury50@gmail.com last updated on 06/May/18
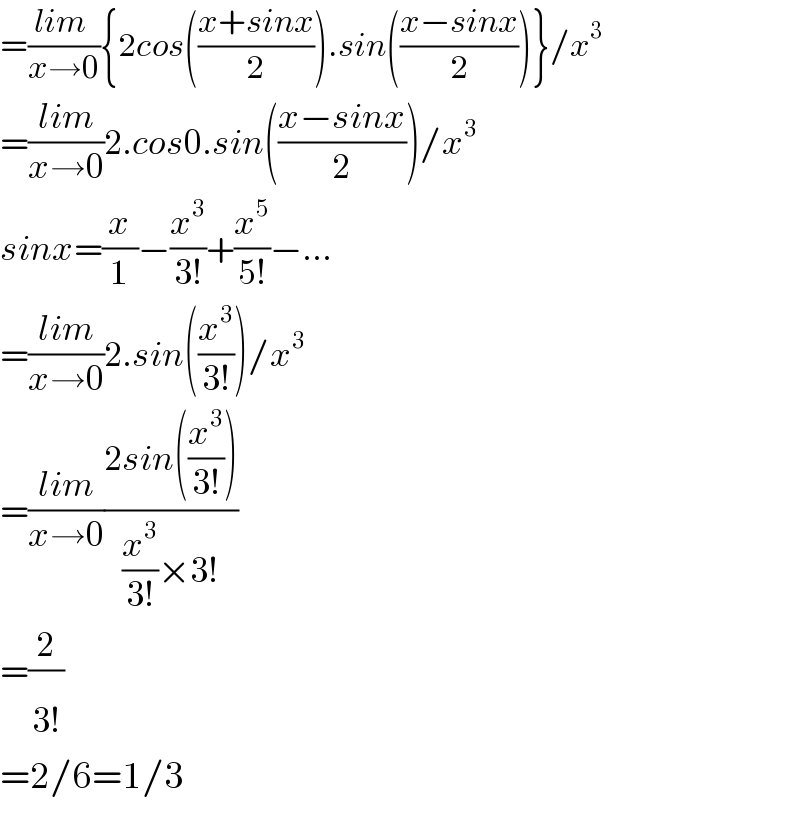
=((lim )/(x→0)){2cos(((x+sinx)/2)).sin(((x−sinx)/2))}/x^3 =((lim)/(x→0))2.cos0.sin(((x−sinx)/2))/x^3 sinx=(x/1)−(x^3 /(3!))+(x^5 /(5!))−... =((lim)/(x→0))2.sin((x^3 /(3!)))/x^3 =((lim)/(x→0))((2sin((x^3 /(3!))))/((x^3 /(3!))×3!)) =(2/(3!^ )) =2/6=1/3
$$=\frac{{lim}\:}{{x}\rightarrow\mathrm{0}}\left\{\mathrm{2}{cos}\left(\frac{{x}+{sinx}}{\mathrm{2}}\right).{sin}\left(\frac{{x}−{sinx}}{\mathrm{2}}\right)\right\}/{x}^{\mathrm{3}} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\mathrm{2}.{cos}\mathrm{0}.{sin}\left(\frac{{x}−{sinx}}{\mathrm{2}}\right)/{x}^{\mathrm{3}} \\ $$$${sinx}=\frac{{x}}{\mathrm{1}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−… \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\mathrm{2}.{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)/{x}^{\mathrm{3}} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\frac{\mathrm{2}{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right)}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}×\mathrm{3}!} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}\overset{} {!}} \\ $$$$=\mathrm{2}/\mathrm{6}=\mathrm{1}/\mathrm{3} \\ $$
Commented by MJS last updated on 06/May/18
something went wrong...
$$\mathrm{something}\:\mathrm{went}\:\mathrm{wrong}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/May/18
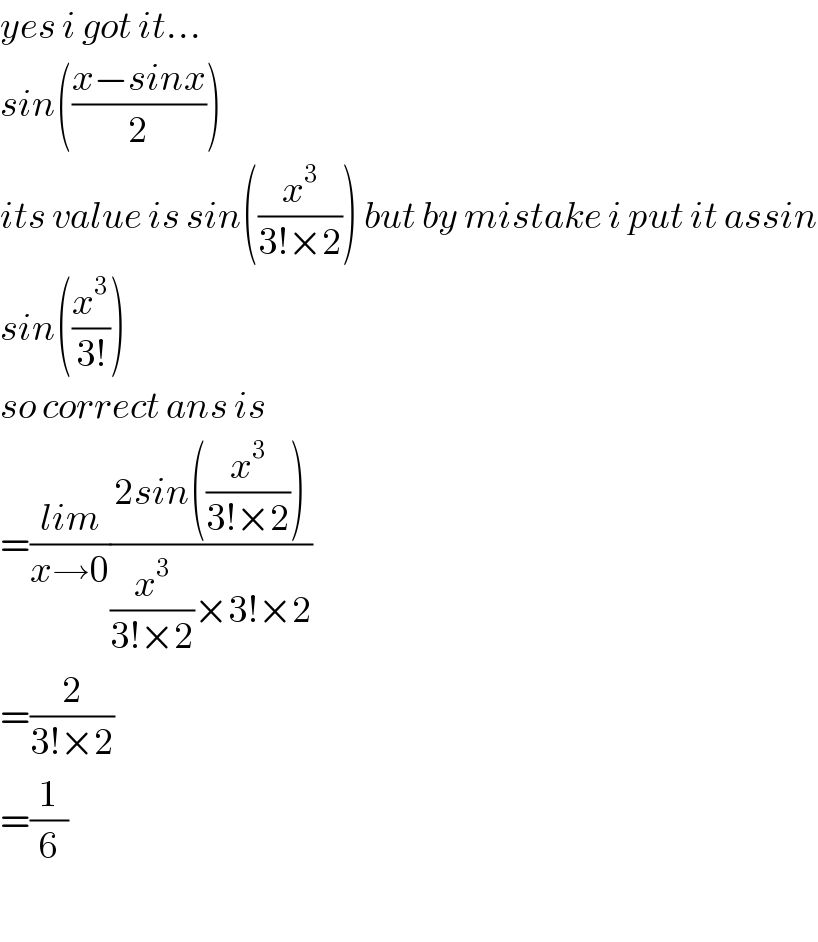
yes i got it... sin(((x−sinx)/2)) its value is sin((x^3 /(3!×2))) but by mistake i put it assin sin((x^3 /(3!))) so correct ans is =((lim)/(x→0))((2sin((x^3 /(3!×2))))/((x^3 /(3!×2))×3!×2)) =(2/(3!×2)) =(1/6)
$${yes}\:{i}\:{got}\:{it}… \\ $$$${sin}\left(\frac{{x}−{sinx}}{\mathrm{2}}\right) \\ $$$${its}\:{value}\:{is}\:{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!×\mathrm{2}}\right)\:{but}\:{by}\:{mistake}\:{i}\:{put}\:{it}\:{assin} \\ $$$${sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\right) \\ $$$${so}\:{correct}\:{ans}\:{is} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{0}}\frac{\mathrm{2}{sin}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!×\mathrm{2}}\right)}{\frac{{x}^{\mathrm{3}} }{\mathrm{3}!×\mathrm{2}}×\mathrm{3}!×\mathrm{2}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}!×\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 07/May/18
Thank you sir! There is also an option for "edit post" ��
Answered by MJS last updated on 06/May/18
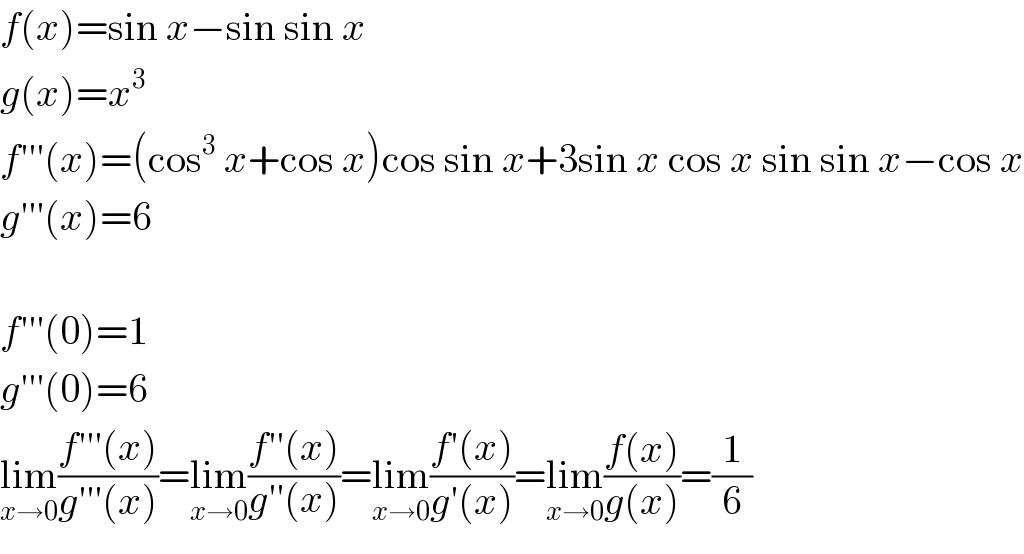
f(x)=sin x−sin sin x g(x)=x^3 f′′′(x)=(cos^3 x+cos x)cos sin x+3sin x cos x sin sin x−cos x g′′′(x)=6 f′′′(0)=1 g′′′(0)=6 lim_(x→0) ((f′′′(x))/(g′′′(x)))=lim_(x→0) ((f′′(x))/(g′′(x)_ ))=lim_(x→0) ((f′(x))/(g′(x)))=lim_(x→0) ((f(x))/(g(x)))=(1/6)
$${f}\left({x}\right)=\mathrm{sin}\:{x}−\mathrm{sin}\:\mathrm{sin}\:{x} \\ $$$${g}\left({x}\right)={x}^{\mathrm{3}} \\ $$$${f}'''\left({x}\right)=\left(\mathrm{cos}^{\mathrm{3}} \:{x}+\mathrm{cos}\:{x}\right)\mathrm{cos}\:\mathrm{sin}\:{x}+\mathrm{3sin}\:{x}\:\mathrm{cos}\:{x}\:\mathrm{sin}\:\mathrm{sin}\:{x}−\mathrm{cos}\:{x} \\ $$$${g}'''\left({x}\right)=\mathrm{6} \\ $$$$ \\ $$$${f}'''\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${g}'''\left(\mathrm{0}\right)=\mathrm{6} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}'''\left({x}\right)}{{g}'''\left({x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}''\left({x}\right)}{{g}''\left({x}\underset{} {\right)}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by rahul 19 last updated on 07/May/18
Thank you sir !

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *