Question Number 79065 by Khyati last updated on 22/Jan/20
![]. lim_(x→0) (([sin(α+β)x+sin(α−β)x+sin2αx)/(cos2βx−cos2αx)).x](https://www.tinkutara.com/question/Q79065.png)
$$\left.\right].\:{li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\:\frac{\left[{sin}\left(\alpha+\beta\right){x}+{sin}\left(\alpha−\beta\right){x}+{sin}\mathrm{2}\alpha{x}\right.}{{cos}\mathrm{2}\beta{x}−{cos}\mathrm{2}\alpha{x}}.{x} \\ $$
Commented by jagoll last updated on 22/Jan/20
![lim_(x→0) (([sin (α+β)x+sin (α−β)x+sin 2αx])/(cos 2βx−cos 2αx))× x?](https://www.tinkutara.com/question/Q79068.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[\mathrm{sin}\:\left(\alpha+\beta\right)\mathrm{x}+\mathrm{sin}\:\left(\alpha−\beta\right)\mathrm{x}+\mathrm{sin}\:\mathrm{2}\alpha\mathrm{x}\right]}{\mathrm{cos}\:\mathrm{2}\beta\mathrm{x}−\mathrm{cos}\:\mathrm{2}\alpha\mathrm{x}}×\:\mathrm{x}? \\ $$
Commented by mathmax by abdo last updated on 22/Jan/20
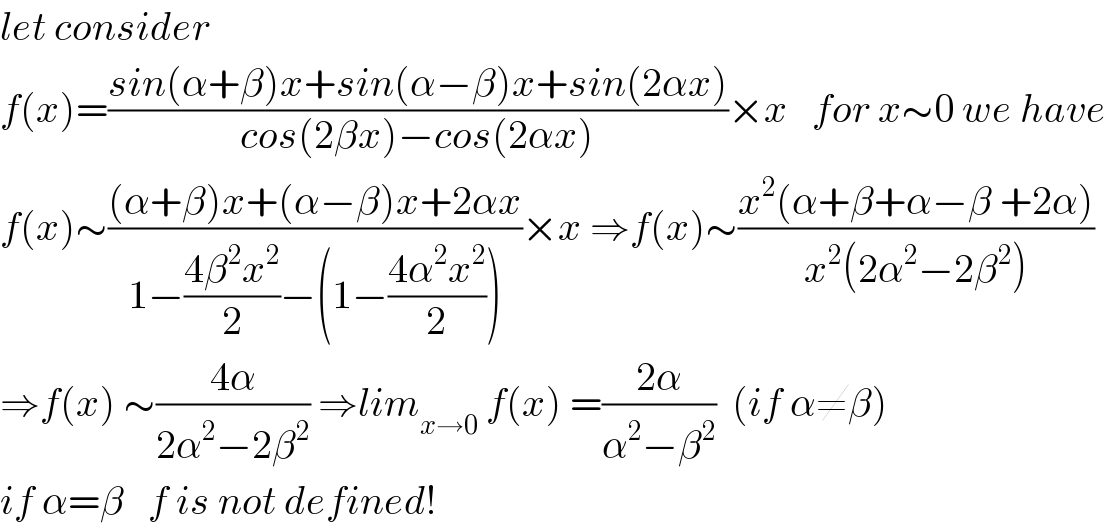
$${let}\:{consider} \\ $$$${f}\left({x}\right)=\frac{{sin}\left(\alpha+\beta\right){x}+{sin}\left(\alpha−\beta\right){x}+{sin}\left(\mathrm{2}\alpha{x}\right)}{{cos}\left(\mathrm{2}\beta{x}\right)−{cos}\left(\mathrm{2}\alpha{x}\right)}×{x}\:\:\:{for}\:{x}\sim\mathrm{0}\:{we}\:{have} \\ $$$${f}\left({x}\right)\sim\frac{\left(\alpha+\beta\right){x}+\left(\alpha−\beta\right){x}+\mathrm{2}\alpha{x}}{\mathrm{1}−\frac{\mathrm{4}\beta^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}}−\left(\mathrm{1}−\frac{\mathrm{4}\alpha^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}}\right)}×{x}\:\Rightarrow{f}\left({x}\right)\sim\frac{{x}^{\mathrm{2}} \left(\alpha+\beta+\alpha−\beta\:+\mathrm{2}\alpha\right)}{{x}^{\mathrm{2}} \left(\mathrm{2}\alpha^{\mathrm{2}} −\mathrm{2}\beta^{\mathrm{2}} \right)} \\ $$$$\Rightarrow{f}\left({x}\right)\:\sim\frac{\mathrm{4}\alpha}{\mathrm{2}\alpha^{\mathrm{2}} −\mathrm{2}\beta^{\mathrm{2}} }\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right)\:=\frac{\mathrm{2}\alpha}{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }\:\:\left({if}\:\alpha\neq\beta\right) \\ $$$${if}\:\alpha=\beta\:\:\:{f}\:{is}\:{not}\:{defined}! \\ $$
Commented by jagoll last updated on 23/Jan/20
![lim_(x→0) ((x[2sin αxcos βx+sin 2αx])/(−2sin (α+β)x sin (β−α)x)) = lim_(x→0) ((2xsin αx+xsin 2αx)/(−2sin (α+β)x.sin (β−α)x))= ((4α)/((α+β)(α−β)))×(1/2)=((2α)/(α^2 −β^2 ))](https://www.tinkutara.com/question/Q79141.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\left[\mathrm{2sin}\:\alpha\mathrm{xcos}\:\beta\mathrm{x}+\mathrm{sin}\:\mathrm{2}\alpha\mathrm{x}\right]}{−\mathrm{2sin}\:\left(\alpha+\beta\right)\mathrm{x}\:\mathrm{sin}\:\left(\beta−\alpha\right)\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2xsin}\:\alpha\mathrm{x}+\mathrm{xsin}\:\mathrm{2}\alpha\mathrm{x}}{−\mathrm{2sin}\:\left(\alpha+\beta\right)\mathrm{x}.\mathrm{sin}\:\left(\beta−\alpha\right)\mathrm{x}}= \\ $$$$\frac{\mathrm{4}\alpha}{\left(\alpha+\beta\right)\left(\alpha−\beta\right)}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}\alpha}{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} }\: \\ $$
Commented by Khyati last updated on 23/Jan/20
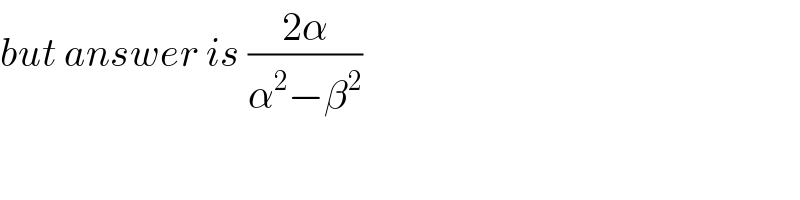
$${but}\:{answer}\:{is}\:\frac{\mathrm{2}\alpha}{\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} } \\ $$
Commented by jagoll last updated on 23/Jan/20

$$\mathrm{yes}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{correct}\:\mathrm{my}\:\mathrm{typo} \\ $$
