Question Number 115777 by bemath last updated on 28/Sep/20

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−\mathrm{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} \:\mathrm{ln}\:\left(\mathrm{1}+{x}\right)} \\ $$
Answered by bobhans last updated on 28/Sep/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{Px}^{\mathrm{5}} \right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{Qx}^{\mathrm{5}} \right)}{{x}^{\mathrm{2}} \left({x}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{Rx}^{\mathrm{3}} \right)}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} +\left({P}−{Q}\right){x}^{\mathrm{5}} }{{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} +{Rx}^{\mathrm{5}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{6}}+\left({P}−{Q}\right){x}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}+{Rx}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by Olaf last updated on 28/Sep/20
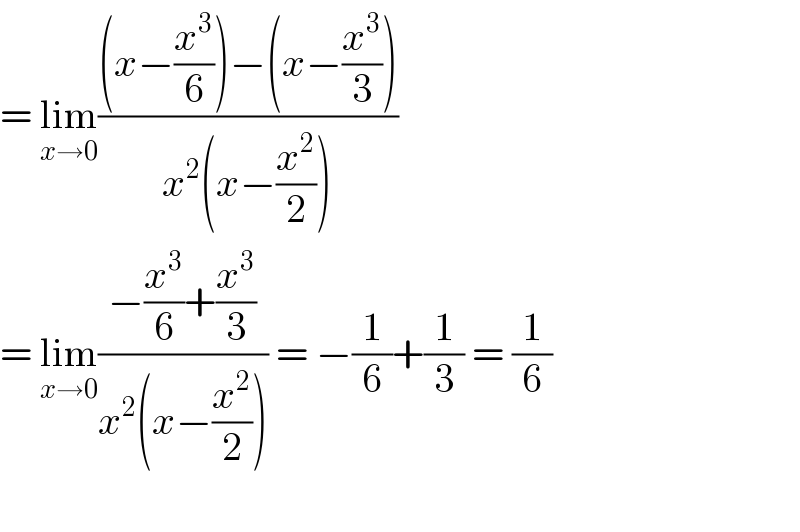
$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)}{{x}^{\mathrm{2}} \left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{{x}^{\mathrm{2}} \left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 28/Sep/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)}{\mathrm{x}^{\mathrm{2}} .\mathrm{x}}=\frac{\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)=\mathrm{x} \\ $$
