Menu Close

lim-x-0-sin-x-x-1-x-2-

Tinku Tara 0 Comments
Pin




Question Number 116576 by bemath last updated on 05/Oct/20
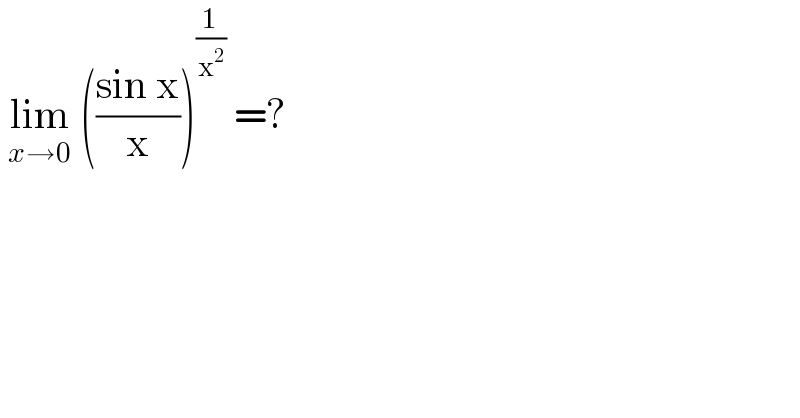
lim_(x→0) (((sin x)/x))^(1/x^2 ) =?
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:=? \\ $$
Commented by mathmax by abdo last updated on 05/Oct/20
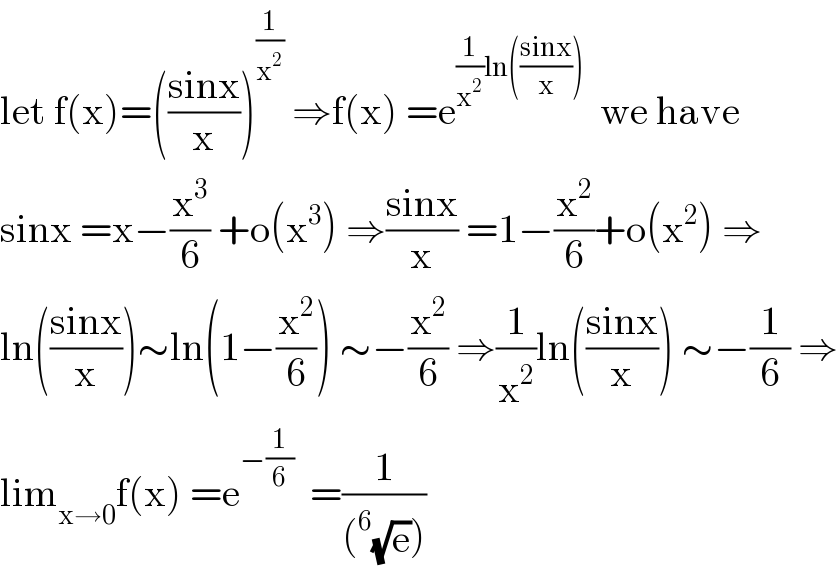
let f(x)=(((sinx)/x))^(1/x^2 ) ⇒f(x) =e^((1/x^2 )ln(((sinx)/x))) we have sinx =x−(x^3 /6) +o(x^3 ) ⇒((sinx)/x) =1−(x^2 /6)+o(x^2 ) ⇒ ln(((sinx)/x))∼ln(1−(x^2 /6)) ∼−(x^2 /6) ⇒(1/x^2 )ln(((sinx)/x)) ∼−(1/6) ⇒ lim_(x→0) f(x) =e^(−(1/6)) =(1/((^6 (√e))))
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)} \:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{sinx}\:=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)\:\Rightarrow\frac{\mathrm{sinx}}{\mathrm{x}}\:=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{ln}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\sim\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)\:\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\:\sim−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:\:=\frac{\mathrm{1}}{\left(^{\mathrm{6}} \sqrt{\mathrm{e}}\right)} \\ $$
Answered by Olaf last updated on 05/Oct/20
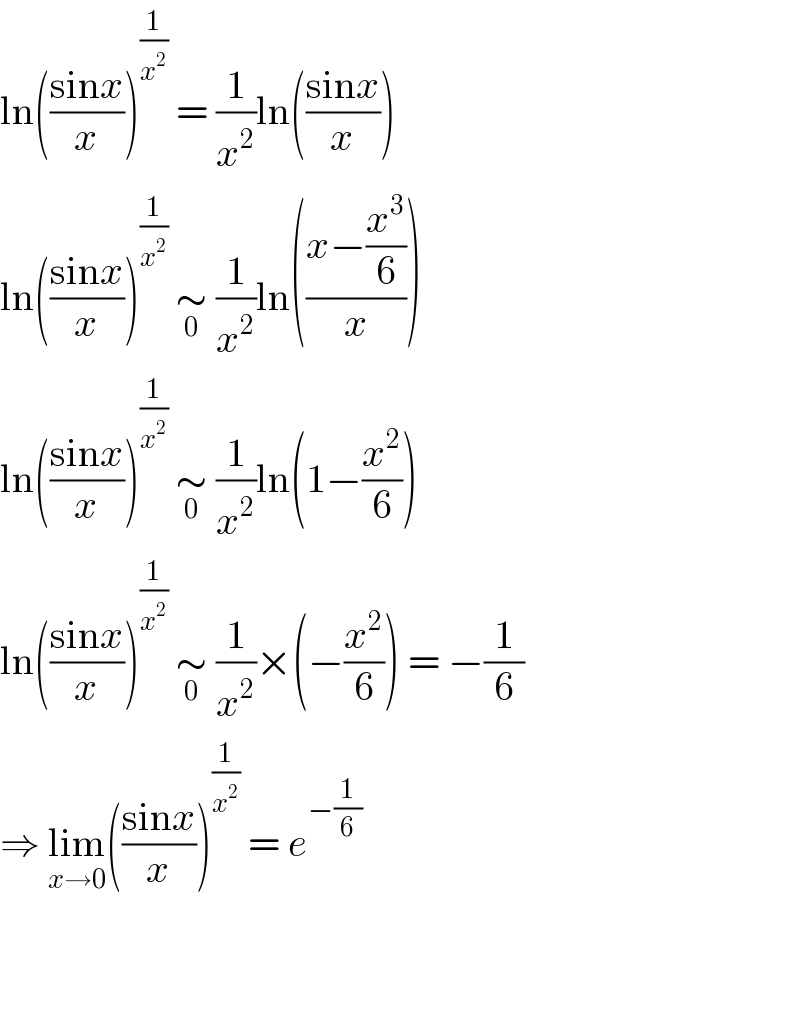
ln(((sinx)/x))^(1/x^2 ) = (1/x^2 )ln(((sinx)/x)) ln(((sinx)/x))^(1/x^2 ) ∼_0 (1/x^2 )ln(((x−(x^3 /6))/x)) ln(((sinx)/x))^(1/x^2 ) ∼_0 (1/x^2 )ln(1−(x^2 /6)) ln(((sinx)/x))^(1/x^2 ) ∼_0 (1/x^2 )×(−(x^2 /6)) = −(1/6) ⇒ lim_(x→0) (((sinx)/x))^(1/x^2 ) = e^(−(1/6))
$$\mathrm{ln}\left(\frac{\mathrm{sin}{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{sin}{x}}{{x}}\right) \\ $$$$\mathrm{ln}\left(\frac{\mathrm{sin}{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{{x}}\right) \\ $$$$\mathrm{ln}\left(\frac{\mathrm{sin}{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right) \\ $$$$\mathrm{ln}\left(\frac{\mathrm{sin}{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }×\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$ \\ $$$$ \\ $$
Answered by bobhans last updated on 05/Oct/20
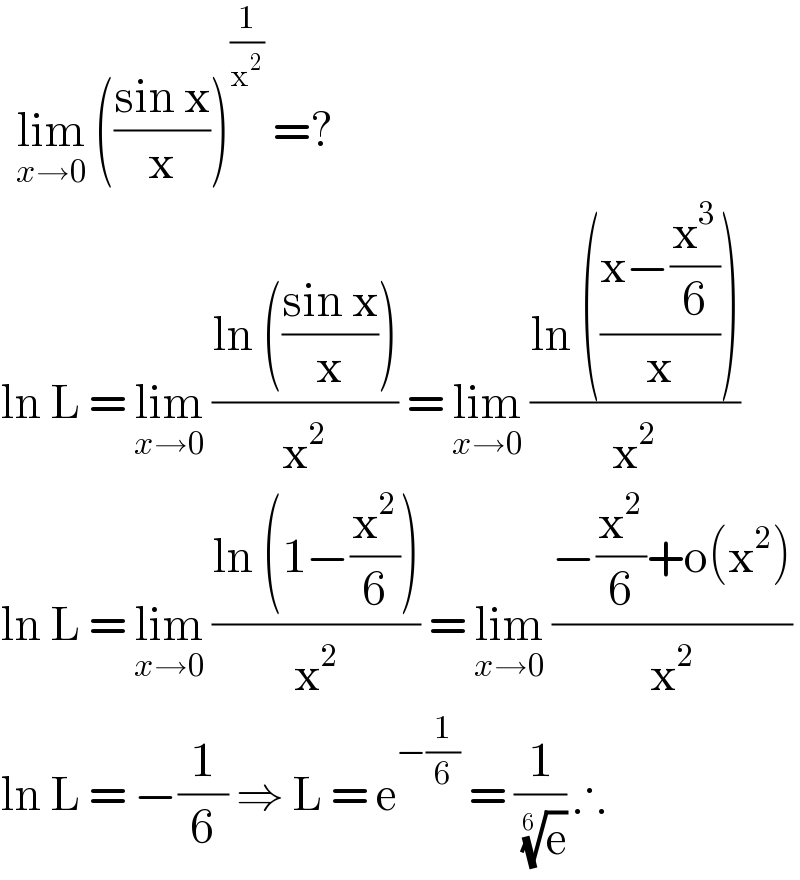
lim_(x→0) (((sin x)/x))^(1/x^2 ) =? ln L = lim_(x→0) ((ln (((sin x)/x)))/x^2 ) = lim_(x→0) ((ln (((x−(x^3 /6))/x)))/x^2 ) ln L = lim_(x→0) ((ln (1−(x^2 /6)))/x^2 ) = lim_(x→0) ((−(x^2 /6)+o(x^2 ))/x^2 ) ln L = −(1/6) ⇒ L = e^(−(1/6)) = (1/( (e)^(1/(6 )) )) ∴
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:=? \\ $$$$\mathrm{ln}\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\frac{\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)}{\mathrm{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:\mathrm{L}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\:\mathrm{L}\:=\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{6}\:}]{\mathrm{e}}}\:\therefore \\ $$
Answered by 1549442205PVT last updated on 05/Oct/20
Put A= lim (((sin x)/x))^(1/x^2 ) ⇒lnI=lim_(x→0) [(1/x^2 )ln(((sinx)/x))]=lim_(x→0) ((ln(((sinx)/x)))/x^2 ) This is the form (0/0)hence using L′Hopital we get lim_(x→0) (((x/(sinx))×((xcosx−sinx)/x^2 ))/(2x))=lim_(x→0) ((xcosx−sinx)/(2x^2 sinx)) = _(L′Hopital) lim_(x→0) ((cosx−xsinx−cosx)/(4xsinx+2x^2 cosx)) = _(L′Hopital) lim_(x→0) ((−sinx)/(4sinx+2xcosx))=lim_(x→0) ((−cosx)/(4cosx+2cosx−2xsinx)) =((−1)/(4+2−0))=((−1)/6) ⇒I=e^((−1)/6) =(1/( ^6 (√e)))
$$\mathrm{Put}\:\mathrm{A}=\:\mathrm{lim}\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{lnI}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\right]=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{form}\:\frac{\mathrm{0}}{\mathrm{0}}\mathrm{hence}\:\mathrm{using}\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{we}\:\mathrm{get} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{x}}{\mathrm{sinx}}×\frac{\mathrm{xcosx}−\mathrm{sinx}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{2x}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{xcosx}−\mathrm{sinx}}{\mathrm{2x}^{\mathrm{2}} \mathrm{sinx}} \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}} {=\:\:\:\:\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cosx}−\mathrm{xsinx}−\mathrm{cosx}}{\mathrm{4xsinx}+\mathrm{2x}^{\mathrm{2}} \mathrm{cosx}} \\ $$$$\underset{\mathrm{L}'\mathrm{Hopital}} {=\:\:\:}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sinx}}{\mathrm{4sinx}+\mathrm{2xcosx}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{cosx}}{\mathrm{4cosx}+\mathrm{2cosx}−\mathrm{2xsinx}}\: \\ $$$$=\frac{−\mathrm{1}}{\mathrm{4}+\mathrm{2}−\mathrm{0}}=\frac{−\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{I}=\mathrm{e}^{\frac{−\mathrm{1}}{\mathrm{6}}} =\frac{\mathrm{1}}{\:\:^{\mathrm{6}} \sqrt{\mathrm{e}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *