Question Number 80653 by jagoll last updated on 05/Feb/20
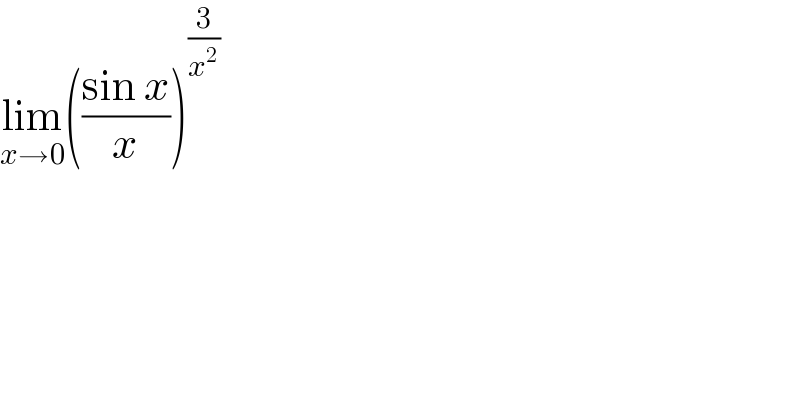
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }} \\ $$
Commented by john santu last updated on 05/Feb/20
![lim_(x→0) (1+(((sin x)/x)−1))^(3/x^2 ) = lim_(x→0) [(1+((sin x−x)/x))^(x/(sin x−x)) ]^((3(sin x−x))/x^3 ) = e^(lim_(x→0) (((3(sin x−x))/x^3 ))) = e^(lim_(x→0) (((3(cos x−1))/(3x^2 )))) = e^(lim_(x→0) (((−sin x)/(2x)))) = e^(−(1/2)) =(1/( (√e)))](https://www.tinkutara.com/question/Q80654.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\frac{\mathrm{sin}\:{x}}{{x}}−\mathrm{1}\right)\right)^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }} = \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{sin}\:{x}−{x}}{{x}}\right)^{\frac{{x}}{\mathrm{sin}\:{x}−{x}}} \right]^{\frac{\mathrm{3}\left(\mathrm{sin}\:{x}−{x}\right)}{{x}^{\mathrm{3}} }} = \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{3}\left(\mathrm{sin}\:{x}−{x}\right)}{{x}^{\mathrm{3}} }\right)} \:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{3}\left(\mathrm{cos}\:{x}−\mathrm{1}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\right)} = \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{−\mathrm{sin}\:{x}}{\mathrm{2}{x}}\right)} \:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Commented by mr W last updated on 05/Feb/20
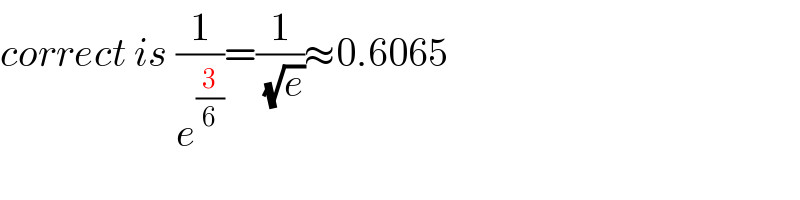
$${correct}\:{is}\:\frac{\mathrm{1}}{{e}^{\frac{\mathrm{3}}{\mathrm{6}}} }=\frac{\mathrm{1}}{\:\sqrt{{e}}}\approx\mathrm{0}.\mathrm{6065} \\ $$
Commented by john santu last updated on 05/Feb/20

$${oo}\:{yes} \\ $$
Commented by jagoll last updated on 05/Feb/20
$${thank}\:{you}\:{mr}\:{W}\:{and}\:{john} \\ $$
Commented by abdomathmax last updated on 05/Feb/20
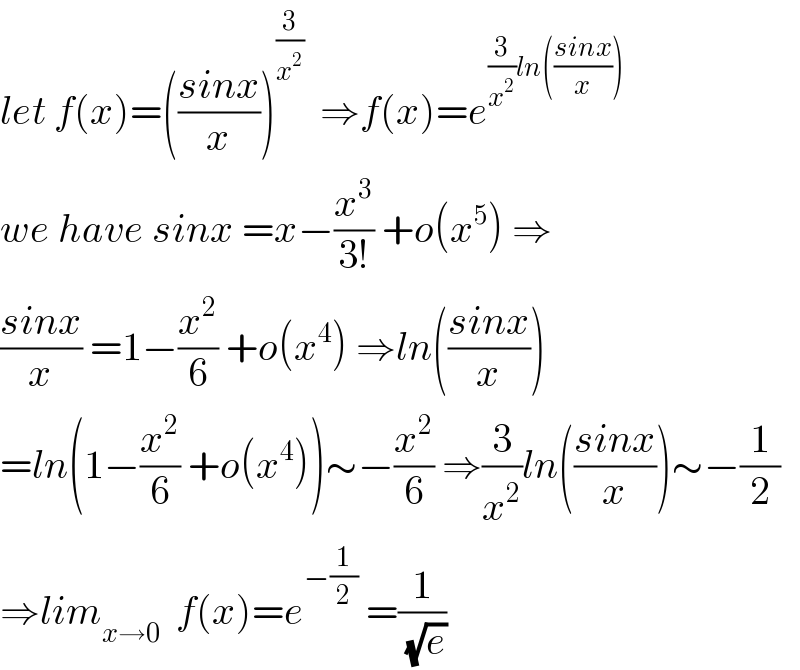
$${let}\:{f}\left({x}\right)=\left(\frac{{sinx}}{{x}}\right)^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }} \:\:\Rightarrow{f}\left({x}\right)={e}^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{sinx}}{{x}}\right)} \\ $$$${we}\:{have}\:{sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow \\ $$$$\frac{{sinx}}{{x}}\:=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow{ln}\left(\frac{{sinx}}{{x}}\right) \\ $$$$={ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\right)\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow\frac{\mathrm{3}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{sinx}}{{x}}\right)\sim−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)={e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
