Question Number 18627 by Arnab Maiti last updated on 26/Jul/17
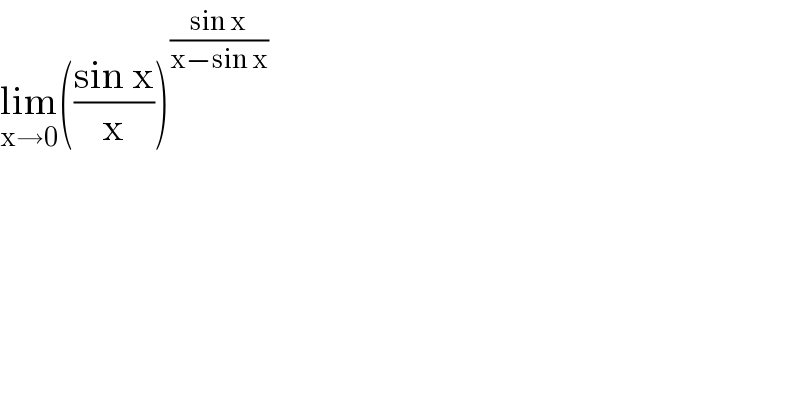
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)^{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}} \\ $$
Commented by Arnab Maiti last updated on 26/Jul/17

$$\mathrm{Please}\:\mathrm{help}. \\ $$
Answered by 433 last updated on 26/Jul/17
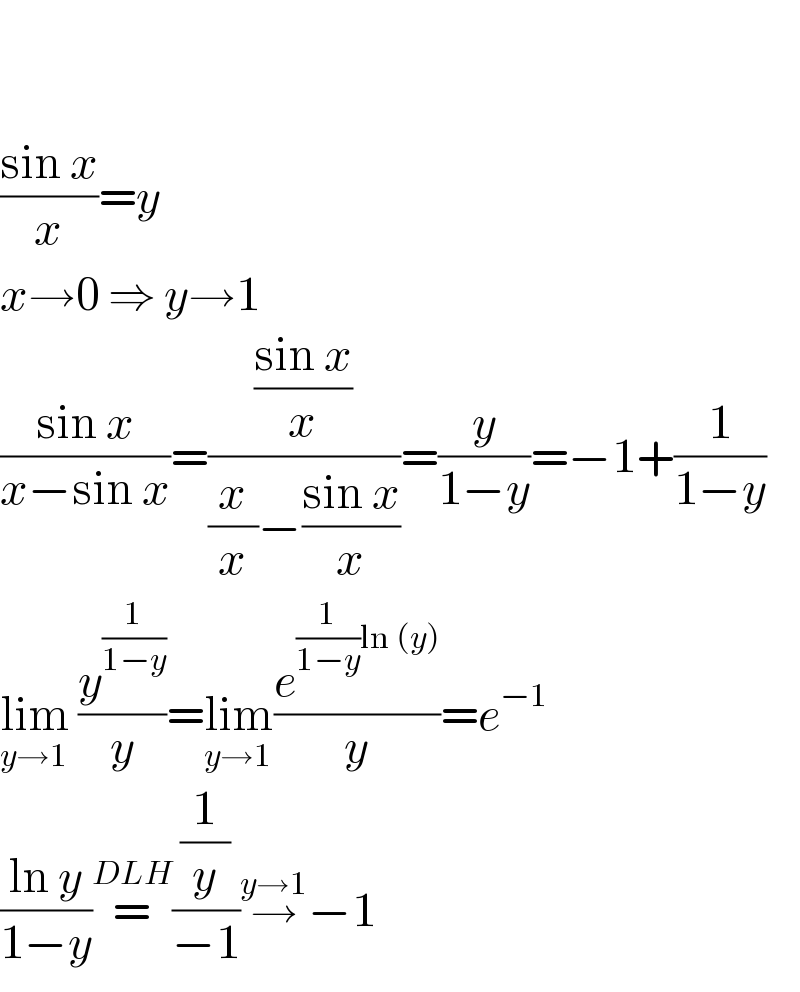
$$ \\ $$$$ \\ $$$$\frac{\mathrm{sin}\:{x}}{{x}}={y} \\ $$$${x}\rightarrow\mathrm{0}\:\Rightarrow\:{y}\rightarrow\mathrm{1} \\ $$$$\frac{\mathrm{sin}\:{x}}{{x}−\mathrm{sin}\:{x}}=\frac{\frac{\mathrm{sin}\:{x}}{{x}}}{\frac{{x}}{{x}}−\frac{\mathrm{sin}\:{x}}{{x}}}=\frac{{y}}{\mathrm{1}−{y}}=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}−{y}} \\ $$$$\underset{{y}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{y}^{\frac{\mathrm{1}}{\mathrm{1}−{y}}} }{{y}}=\underset{{y}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{\frac{\mathrm{1}}{\mathrm{1}−{y}}\mathrm{ln}\:\left({y}\right)} }{{y}}={e}^{−\mathrm{1}} \\ $$$$\frac{\mathrm{ln}\:{y}}{\mathrm{1}−{y}}\overset{{DLH}} {=}\frac{\frac{\mathrm{1}}{{y}}}{−\mathrm{1}}\overset{{y}\rightarrow\mathrm{1}} {\rightarrow}−\mathrm{1} \\ $$
