Question Number 114539 by naka3546 last updated on 19/Sep/20
![lim_(x→0) [ ((sinh x − sin x)/x^3 ) ] = ?](https://www.tinkutara.com/question/Q114539.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left[\:\frac{\mathrm{sinh}\:{x}\:−\:\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\:\right]\:\:=\:\:? \\ $$
Commented by bemath last updated on 20/Sep/20
![lim_(x→0) (((1/2)[(1+x+(x^2 /2)+(x^3 /6))−(1−x+(x^2 /2)−(x^3 /6))]−(x−(x^3 /6)))/x^3 ) lim_(x→0) (((1/2)(2x+(x^3 /3))−(x−(x^3 /6)))/x^3 ) lim_(x→0) (((2/6)x^3 )/x^3 ) = (1/3).](https://www.tinkutara.com/question/Q114695.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)\right]−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{2}}{\mathrm{6}}{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}. \\ $$
Answered by bobhans last updated on 19/Sep/20
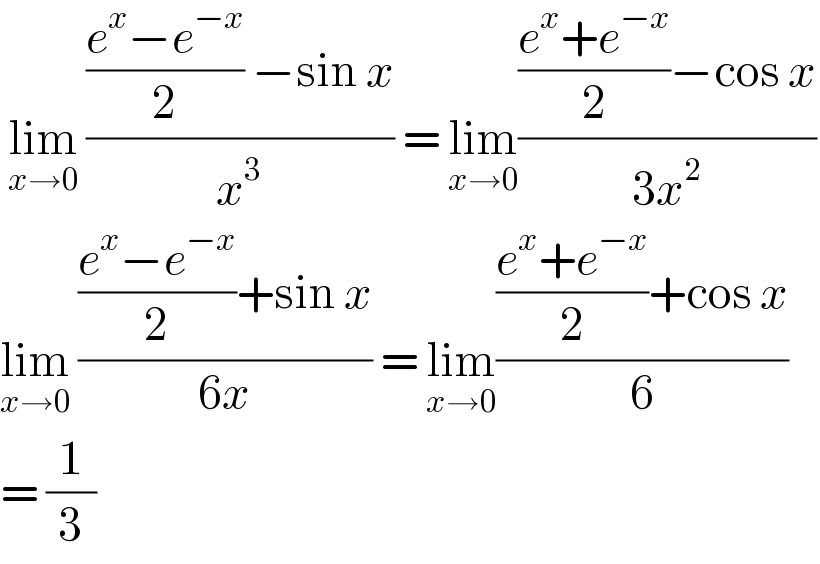
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}\:−\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}−\mathrm{cos}\:{x}}{\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}+\mathrm{sin}\:{x}}{\mathrm{6}{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}+\mathrm{cos}\:{x}}{\mathrm{6}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Sep/20
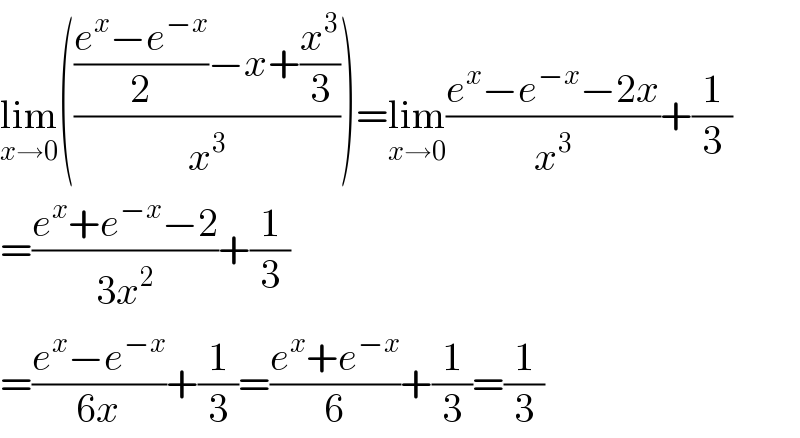
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{{x}^{\mathrm{3}} }\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{−{x}} −\mathrm{2}{x}}{{x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{{e}^{{x}} +{e}^{−{x}} −\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{6}{x}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
